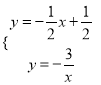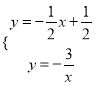ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΒ±ΆΦ–ΈΨΏ”–ΝΎ±ΏœύΒ»ΒΡΧΊ’ς ±Θ§Έ“Ο«Ω…“‘Α―ΆΦ–ΈΒΡ“Μ≤ΩΖ÷»ΤΉ≈ΙΪΙ≤ΕΥΒψ–ΐΉΣΘ§’β―υΫΪΖ÷…ΔΒΡΧθΦΰΦ·÷–Τπά¥Θ§¥”Εχ¥οΒΫΫβΨωΈ ΧβΒΡΡΩΒΡ
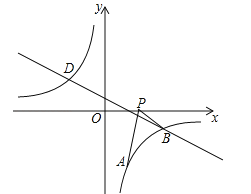
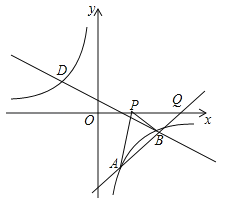
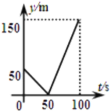
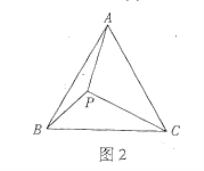
![]() »γΆΦ1Θ§Β»―ϋ÷±Ϋ«»ΐΫ«–Έ
»γΆΦ1Θ§Β»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() ΡΎ”–“ΜΒψ
ΡΎ”–“ΜΒψ![]() Ν§Ϋ”
Ν§Ϋ”![]() ΈΣΧΫΨΩ
ΈΣΧΫΨΩ![]() »ΐΧθœΏΕΈΦδΒΡ ΐΝΩΙΊœΒΘ§Έ“Ο«Ω…“‘ΫΪ
»ΐΧθœΏΕΈΦδΒΡ ΐΝΩΙΊœΒΘ§Έ“Ο«Ω…“‘ΫΪ![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ
Ρφ ±’κ–ΐΉΣ![]() ΒΟΒΫ
ΒΟΒΫ![]() Ν§Ϋ”
Ν§Ϋ”![]() ‘ρ
‘ρ![]() ___ ____
___ ____![]() «_ »ΐΫ«–ΈΘ§
«_ »ΐΫ«–ΈΘ§![]() »ΐΧθœΏΕΈΒΡ ΐΝΩΙΊœΒ «_ ΘΜ
»ΐΧθœΏΕΈΒΡ ΐΝΩΙΊœΒ «_ ΘΜ
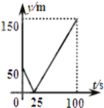
![]() »γΆΦ2Θ§Β»±Ώ»ΐΫ«–Έ
»γΆΦ2Θ§Β»±Ώ»ΐΫ«–Έ![]() ΡΎ“ΜΒψPΘ§Ν§Ϋ”
ΡΎ“ΜΒψPΘ§Ν§Ϋ”![]() «κΫη÷ζΒΎ“ΜΈ ΒΡΖΫΖ®ΧΫΨΩ
«κΫη÷ζΒΎ“ΜΈ ΒΡΖΫΖ®ΧΫΨΩ![]() »ΐΧθœΏΕΈΦδΒΡ ΐΝΩΙΊœΒΘ°
»ΐΧθœΏΕΈΦδΒΡ ΐΝΩΙΊœΒΘ°
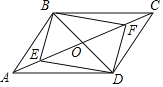
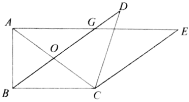
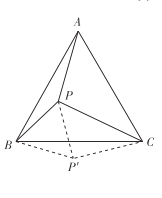
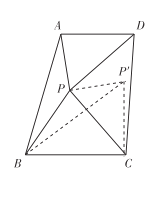
ΓΨ¥πΑΗΓΩΘ®1Θ© ΓΨΫβΈωΓΩ Θ®1Θ©ΗυΨί–ΐΉΣΒΡ–‘÷ “ΉΒΟ Θ®2Θ©ΫΪ Θ®3Θ©ΫΪ Γύ Γύ ΓΏBPΓΆ Γύ Γύ Φ¥ ‘ρ ‘ρ ‘Ύ Ω…÷Λ ‘ρ![]() »γΆΦ3 Θ§‘ΎΥΡ±Ώ–Έ
»γΆΦ3 Θ§‘ΎΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() Βψ
Βψ![]() ‘ΎΥΡ±Ώ–ΈΡΎ≤ΩΘ§«“
‘ΎΥΡ±Ώ–ΈΡΎ≤ΩΘ§«“![]()
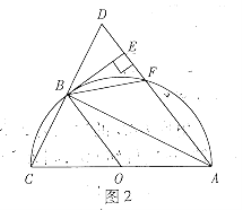
![]() «κ÷±Ϋ”–¥≥ω
«κ÷±Ϋ”–¥≥ω![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°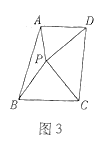
![]() Θ§÷±Ϋ«Θ§
Θ§÷±Ϋ«Θ§![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ§÷ΛΟςœξΦϊΫβΈωΘΜΘ®3Θ©
Θ§÷ΛΟςœξΦϊΫβΈωΘΜΘ®3Θ©![]()
![]()
![]() Θ§
Θ§![]() «÷±Ϋ«»ΐΫ«–ΈΘ§‘ΌΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…«σΫβ.
«÷±Ϋ«»ΐΫ«–ΈΘ§‘ΌΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…«σΫβ.![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() ΒΟ
ΒΟ![]() Ν§Ϋ”
Ν§Ϋ”![]() Ω…ΒΟ
Ω…ΒΟ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§![]() Θ§‘ΌΗυΨί
Θ§‘ΌΗυΨί![]() άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…«σΫβ.
άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…«σΫβ.![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() ÷Ν
÷Ν![]() Ν§Ϋ”
Ν§Ϋ”![]() ‘ρ
‘ρ![]() Θ§ΗυΨί
Θ§ΗυΨί![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Θ§‘ΌΗυΨί
Θ§‘ΌΗυΨί![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Φ¥
Φ¥![]() Θ§‘Ύ
Θ§‘Ύ![]() ÷–Ω…«σΒΟ
÷–Ω…«σΒΟ![]() Θ§‘ΌΗυΨί
Θ§‘ΌΗυΨί![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]() Θ§¥”Εχ÷ΛΟς
Θ§¥”Εχ÷ΛΟς![]() Φ¥Ω…«σΫβ.
Φ¥Ω…«σΫβ.![]() ΓΏ
ΓΏ![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ
Ρφ ±’κ–ΐΉΣ![]() ΒΟΒΫ
ΒΟΒΫ![]()
![]() Θ§Γœ
Θ§Γœ![]() =
=![]()
![]()
![]()
![]() «÷±Ϋ«»ΐΫ«–ΈΘ°
«÷±Ϋ«»ΐΫ«–ΈΘ°![]()
![]()
![]()
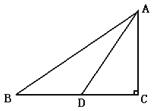
![]() »γΆΦΘ§ΫΪ
»γΆΦΘ§ΫΪ![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() ΒΟ
ΒΟ![]() Ν§Ϋ”
Ν§Ϋ”![]()
![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§![]()
![]()
![]() Θ°
Θ°![]() Θ°ΫΪ
Θ°ΫΪ![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() ÷Ν
÷Ν![]() Ν§Ϋ”
Ν§Ϋ”![]()
![]() Θ°
Θ°![]()
![]() Θ°
Θ°![]() Θ§
Θ§![]() Φ¥
Φ¥![]() Θ°
Θ°![]() ÷–Ω…«σΒΟ
÷–Ω…«σΒΟ![]() Θ°
Θ°![]() Θ§
Θ§![]() Θ°
Θ°![]()
![]() Θ°
Θ°
ΚλΕ‘Ι¥÷–ΩΦΖ÷άύ―ΒΝΖœΒΝ–¥πΑΗ
Κλ…ΪΖ㱩≥θ÷–…ζ―ß“ΒΩΦ ‘ΡΘΡβ”κ‘Λ≤βœΒΝ–¥πΑΗ

÷–ΩΦ–¬Η≈ΡνœΒΝ–¥πΑΗ
ΜΞΝΣΆχΕύΙΠΡήΉς“Β±ΨœΒΝ–¥πΑΗ
ΜΤΗ‘Ϋπ≈Τ÷°¬ΖΟνΫβΫΧ≤ΡœΒΝ–¥πΑΗ
ΜΤΗ‘Ϋπ≈Τ÷°¬Ζ÷–ΩΦΨΪ”ΔΉήΗ¥œΑœΒΝ–¥πΑΗ
÷–ΩΦ–¬Εα±ξ ‘Χβ―–ΨΩœΒΝ–¥πΑΗ
Μψ≤β≥θ÷–”Δ”οœΒΝ–¥πΑΗ
ΜαΩΦΫα“Β―ßœΑ ÷≤αœΒΝ–¥πΑΗ
ΓΨΧβΡΩΓΩ÷”Ρœ…Ϋ‘Κ ΩΧΗΒΫΖάΜΛ–¬–ΆΙΎΉ¥≤ΓΕΨΖΈ―Ή ±ΥΒΘΚΓΑΈ“Ο«–η“Σ÷Ί ”ΖάΜΛΘ§ΒΪ“≤≤Μ±ΊΩ÷Μ≈Θ§ΨΓΝΩ…Ό»Ξ»Υ‘±ΟήΦ·ΒΡ≥ΓΥυΘ§≥ωΟ≈¥ςΩΎ’÷Θ§‘Ύ “ΡΎΉΔ“βΆ®ΖγΘ§«Ύœ¥ ÷Θ§Εύ‘ΥΕ·Θ§…ΌΑΨ“ΙΘ°Γ±Ρ≥…γ«χΈΣΝΥΦ”«Ω…γ«χΨ”ΟώΕ‘–¬–ΆΙΎΉ¥≤ΓΕΨΖΈ―ΉΖάΜΛ÷Σ ΕΒΡΝΥΫβΘ§Ά®ΙΐΈΔ–≈»Κ–ϊ¥Ϊ–¬–ΆΙΎΉ¥≤ΓΕΨΖΈ―ΉΒΡΖάΜΛ÷Σ ΕΘ§≤ΔΙΡάχ…γ«χΨ”Οώ‘ΎœΏ≤Έ”κΉς¥πΓΕ2020Ρξ–¬–ΆΙΎΉ¥≤ΓΕΨΖά÷Έ»ΪΙζΆ≥“ΜΩΦ ‘Θ®»ΪΙζΨμΘ©ΓΖ ‘ΨμΘ®¬ζΖ÷100Ζ÷Θ©Θ§…γ«χΙήάμ‘±ΥφΜζ¥””–400»ΥΒΡΡ≥–Γ«χ≥ι»Γ40Οϊ»Υ‘±ΒΡ¥πΨμ≥…Φ®Θ§≤ΔΕ‘ΥϊΟ«ΒΡ≥…Φ®Θ®ΒΞΈΜΘΚΖ÷Θ©Ά≥ΦΤ»γœ¬ΘΚ
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
ΗυΨί ΐΨίΜφ÷ΤΝΥ»γœ¬ΒΡ±μΗώΚΆΆ≥ΦΤΆΦΘΚ
Β»ΦΕ | ≥…Φ®Θ® | ΤΒ¬ | ΤΒ¬ |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
ΚœΦΤ | 40 | 1 | |
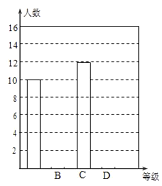
ΗυΨί…œΟφΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©Ά≥ΦΤ±μ÷–ΒΡ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©ΗυΨί≥ι―υΒς≤ιΫαΙϊΘ§«κΙάΦΤΗΟ–Γ«χ¥πΧβ≥…Φ®ΈΣΓΑ![]() ΦΕΓ±ΒΡ”–Εύ…Ό»ΥΘΩ
ΦΕΓ±ΒΡ”–Εύ…Ό»ΥΘΩ
Θ®4Θ©ΗΟ…γ«χ”–2ΟϊΡ–Ιήάμ‘±ΚΆ2Οϊ≈°Ιήάμ‘±Θ§œ÷¥”÷–ΥφΜζΧτ―Γ2ΟϊΙήάμ‘±≤ΈΦ”ΓΑ…γ«χΖάΩΊΓ±–ϊ¥ΪΜνΕ·Θ§«κ”Ο ςΉ¥ΆΦΖ®ΜρΝ–±μΖ®«σ≥ω«ΓΚΟ―Γ÷–ΓΑ1Ρ–1≈°Γ±ΒΡΗ≈¬ Θ°