题目内容
16.某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门也大小相同,安全检查中,对4道门进行了测试,当同时开启一道正门和两道侧门时,2分钟可以通过560名学生,当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生.(1)平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低10%,安全检查规定,在紧急情况下全楼的学生在4分钟内通过这4道门安全撤离,问:这栋教学楼平均每间教室最多多少人?
分析 (1)设平均每分钟一道正门可以通过x名学生,一道侧门可以通过y名学生,根据同时开启一道正门和两道侧门时,2分钟可以通过560名学生,同时开启一道正门和一道侧门时,4分钟内可以通过800名学生,列方程组求解;
(2)设这栋教学楼平均每间教室有m人,根据学生在4分钟内通过这4道门,列不等式求解.
解答 解:(1)设平均每分钟一道正门可以通过x名学生,一道侧门可以通过y名学生,
由题意得,$\left\{\begin{array}{l}{2(x+2y)=560}\\{4(x+y)=800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=120}\\{y=80}\end{array}\right.$,
答:平均每分钟一道正门可以通过120名学生,一道侧门可以通过80名学生;
(2)设这栋教学楼平均每间教室有m人,
由题意得,4×8m≤4×2×(120+80)×(1-10%),
解得:m≤45.
答:这栋教学楼平均每间教室最多有45人.
点评 本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
11. 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )| A. | s1>s2 | B. | 2s1<s2 | C. | s1<s2 | D. | s1=s2 |
8. 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )
如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
6. 如图,小亮从A点出发前进10m,向右转一角度,再前进10m,又向右转一相同角度,…,这样一直走下去,他回到出发点A时,一共走了180m,则他每次转动的角度是( )
如图,小亮从A点出发前进10m,向右转一角度,再前进10m,又向右转一相同角度,…,这样一直走下去,他回到出发点A时,一共走了180m,则他每次转动的角度是( )
 如图,小亮从A点出发前进10m,向右转一角度,再前进10m,又向右转一相同角度,…,这样一直走下去,他回到出发点A时,一共走了180m,则他每次转动的角度是( )
如图,小亮从A点出发前进10m,向右转一角度,再前进10m,又向右转一相同角度,…,这样一直走下去,他回到出发点A时,一共走了180m,则他每次转动的角度是( )| A. | 15° | B. | 18° | C. | 20° | D. | 不能确定 |
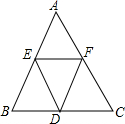 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?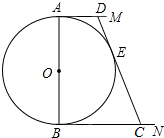 如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.
如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.
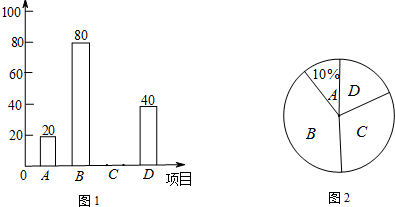
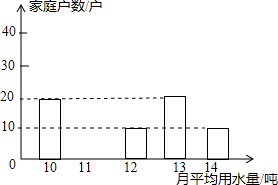 为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况作一次调查.市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况作一次调查.市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.