Question

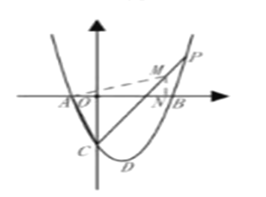
【题目】已知抛物线y＝x2+bx+c与x轴交于A（-1，0）、B两点，与y轴交于点C，OC = 3OA，D为抛物线的顶点．

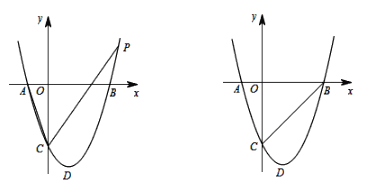
（1）求抛物线的解析式；

（2）若点P在抛物线上，tan∠ACP = ，求P点的坐标；

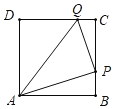
（3）将抛物线沿直线y = x + b翻折，若点D的对应点E落在△ABC的内部（含△ABC的边）时，求b的取值范围．

Answer 1

【答案】(1) y＝x2-2x-3；(2) P(,)；(3) ≤b≤-2．

【解析】

(1)由A（-1，0）和OC = 3OA确定C点坐标,然后使用待定系数法解答即可；

（2）过A作AM⊥AC交CP于M ，tan∠ACP =,则△AOC∽△MNA，有,则,MN=AO=,AN=OC=4,可得ON=AN-AO=3,则M(3, ),再确定CM的解析式,在于抛物线解析式联立即可完成解答;

（3）分E在A上和E在AO与BC的交点两种情况讨论求出临界点即可．

解：∵A（-1，0），OC = 3OA

∴C(0,-3)

则有 即

∴抛物线的解析式为y＝x2-2x-3；

（2）过A作AM⊥AC交CP于M,过M作MN⊥x轴,垂足为N

∴tan∠ACP=

易证∠ACO=∠MAN, ∠AOC=∠MNA,

∴△AOC∽△MNA

∴

∴MN=AO=,AN=OC=4

∴ON=AN-AO=3

∴M(3, )

利用待定系数法可得CM的解析式为:y=

联立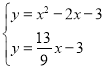 解得 或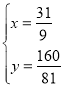

∴P(,)

(3)tan∠ADH=

∴

①E在A上时,DE的中点(0,-3)在y=-x+b上,解得b=-2

②E在AO与BC的交点,BC的解析式为y=x-3;AO的解析式为y=-2x-2

联立可得E(,-)

∴DE的中点为( ,-)在y=-x+b上,解得b=-

∴≤b≤-2