题目内容
17．
一次函数y=kx+b的图象如图，kx+b=0的解为x=2；不等式kx+b＜0的解集为x＞2．
分析 利用函数图象，找出函数值为0时的自变量的值即可得到kx+b=0的解；写出函数图象在x轴下方所对应的自变量的范围即得到不等式kx+b＜0的解集．
解答 解：根据函数图象，当x=2时，y=0，即kx+b=0；
当x＞2时，y＜0，即kx+b＜0，
所以kx+b=0的解为x=2；不等式kx+b＜0的解集为x＞2．
故答案为x=2，x＞2．
点评 本题考查了一次函数与一元一次不等式：一次函数与一元一次不等式的关系从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
相关题目
7．下面计算正确的是（ ）
| A． | -x2-x2=0 | B． | 3a2+2a3=5a5 | C． | 3+x=3x | D． | -ab+ba=0 |
8．若（x-2）（x+3）=x2-ax+b，则a、b的值是（ ）
| A． | a=5，b=6 | B． | a=1，b=-6 | C． | a=-1，b=-6 | D． | a=5，b=-6 |
5．点M（2，1）关于x轴对称的点的坐标是（ ）
| A． | （1，-2） | B． | （-2，1） | C． | （2，-1） | D． | （-1，2） |
”表示数据输入、输出框；用“
”表示数据处理和运算框；用“
”表示数据判断框（根据条件决定执行两条路径中的某一条）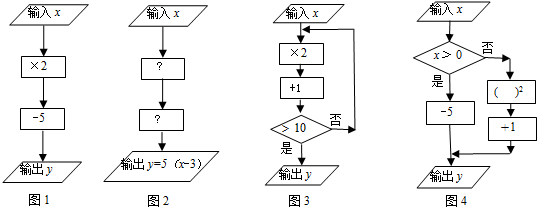
”内，应填-3；第二个运算框“
”内，应填×5；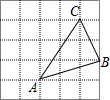
如图，每个小方格都是边长为1个单位的小正方形，A，B，C三点都是格点（每个小方格的顶点叫格点）．
如图是由5个大小相同的小正方体摆成的立体图形，则从正面看得到的平面图形是（ ）
