题目内容
如图,二次函数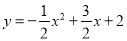 的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
(1)写出线段AC, BC的长度:AC= ,BC= ;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出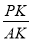 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出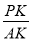 的最大值.
的最大值.
练习册系列答案
相关题目
题目内容
如图,二次函数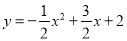 的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
(1)写出线段AC, BC的长度:AC= ,BC= ;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出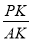 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出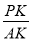 的最大值.
的最大值.