题目内容
2．
如图，点A，M，B，C，N，D在一条直线上，若AB：BC：CD=2：3：2，AB的中点M与CD的中点N的距离是11cm，求AD的长．
分析 设AB=2xcm，BC=3x，CD=2x．由中点的定义可知MB=xcm，NC=xcm，由MN=11cm得x+3x+x=11，求得x的值，从而可求得AD的长．
解答 解：设AB=2xcm，BC=3x，CD=2x．
∵M是AB的中点，
∴MB=xcm．
∵N是CD的中点，
∴NC=xcm．
∵MN=11cm，
∴x+3x+x=11．
解得：x=2.2．
AD=2x+3x+2x=7x=15.4cm．
点评 本题主要考查的是两点间的距离，根据线段中点的定义列出关于x的方程是解题的关键．
练习册系列答案
相关题目
11．
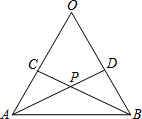如图所示，AO=BO，CO=DO，连接AD、BC，设AD、BC相交于点P．结论：①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．以上结论中（ ）
如图所示，AO=BO，CO=DO，连接AD、BC，设AD、BC相交于点P．结论：①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．以上结论中（ ）| A． | 只有①正确 | B． | 只有②正确 | C． | 只有①②正确 | D． | ①②③都正确 |