题目内容
如图，在城市改造中，市政府欲在一条人工河上架一座桥，河的两岸PQ与MN平行，河岸MN上有A、B两个相距50米的凉亭，小亮在河对岸D处测得∠ADP＝60°，然后沿河岸走了110米到达C处，测得∠BCP＝30°，求这条河的宽．(结果保留根号)
答案：
解析：
解析：
|
作AE⊥PQ于E，CF⊥MN于F．(1分)
∵PQ∥MN， ∴四边形AECF为矩形． ∴EC＝AF，AE＝CF．(2分) 设这条河宽为x米， ∴AE＝CF＝x． 在Rt△AED中， ∵∠ADP＝60°， ∴ED＝ ∵PQ∥MN， ∴∠CBF＝∠BCP＝30°． ∴在Rt△BCF中， BF＝ ∵EC＝ED＋CD，AF＝AB＋BF， ∴ 解得x＝30 ∴这条河的宽为30 |
＝
＝
x．(4分)
＝
＝
x．(6分)
x＋110＝50＋
x．
．
米．(10分)
练习册系列答案
相关题目
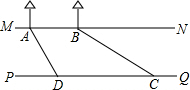（2011•辽阳）如图，在城市改造中，市政府欲在一条人工河上架一座桥，河的两岸PQ与MN平行，河岸MN上有A、B两个相距50米的凉亭，小亮在河对岸D处测得∠ADP=60°，然后沿河岸走了110米到达C处，测得∠BCP=30°，求这条河的宽．（结果保留根号）
