题目内容
13.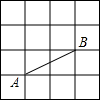 如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )
如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )| A. | $\frac{4}{23}$ | B. | $\frac{6}{23}$ | C. | $\frac{7}{23}$ | D. | $\frac{8}{23}$ |
分析 根据已知条件,可知按照点C所在的直线分两种情况:①点C以点A为标准,AB为底边;②点C以点B为标准,AB为等腰三角形的一条边.
解答  解:如图,∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
解:如图,∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴①若AB=BC,则符合要求的有:C1,C2,C3,C4,C5,共5个点;
②若AB=AC,则符合要求的有:C6,C7,C8共3个点;
若AC=BC,则不存在这样格点.
∴这样的C点有8个.
∴能使△ABC为等腰三角形的概率是$\frac{8}{23}$.
故选D.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
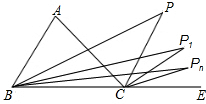 已知BP1平分∠ABC,CP1平分∠ACD;BP2平分∠P1BC,CP2平分∠P1CD;…,如此下去,得到∠Pn和∠A关系为∠Pn=($\frac{1}{2}$)n∠A.
已知BP1平分∠ABC,CP1平分∠ACD;BP2平分∠P1BC,CP2平分∠P1CD;…,如此下去,得到∠Pn和∠A关系为∠Pn=($\frac{1}{2}$)n∠A.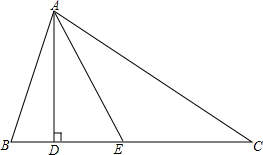 如图,△ABC中,∠B>∠C,AD是高,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,△ABC中,∠B>∠C,AD是高,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).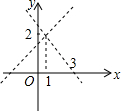 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.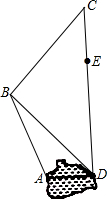 如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.
如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离. 同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )
同桌读了:“子非鱼焉知鱼之乐乎?”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问:由图中所示的图案通过平移后得到的图案是( )



 y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是x>1.
y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是x>1.