ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ ![]() £ђѕяґќ
£ђѕяґќ![]() ‘Џ÷б…ѕ£ђ
‘Џ÷б…ѕ£ђ ![]() =12£ђµг
=12£ђµг![]() µƒ„ш±кќ™(-3,0)£ђѕяґќ
µƒ„ш±кќ™(-3,0)£ђѕяґќ![]() љї
љї![]() ÷б”Џµг
÷б”Џµг![]() £ђєэ
£ђєэ![]() „ч
„ч![]() ”Џ
”Џ![]() £ђґѓµг
£ђґѓµг![]() і”‘≠µг≥цЈҐ£ђ“‘√њ√л3Єцµ•ќїµƒЋўґ»—Ў
і”‘≠µг≥цЈҐ£ђ“‘√њ√л3Єцµ•ќїµƒЋўґ»—Ў![]() ÷бѕт”“‘Ћґѓ£ђ…и‘Ћґѓµƒ ±Љдќ™
÷бѕт”“‘Ћґѓ£ђ…и‘Ћґѓµƒ ±Љдќ™![]() √л.
√л.
(1)µг![]() µƒ„ш±кќ™£®_________£©£ђ__________);
µƒ„ш±кќ™£®_________£©£ђ__________);
(2)µ±![]() «µ»—ь»эљ«–ќ ±£ђ«у
«µ»—ь»эљ«–ќ ±£ђ«у![]() µƒ÷µ;
µƒ÷µ;
(3)»фµг![]() ‘ЋґѓµƒЌђ ±£ђ
‘ЋґѓµƒЌђ ±£ђ ![]() “‘
“‘![]() ќ™ќїЋ∆÷––ƒѕт”“Ј≈іу£ђ«“µг
ќ™ќїЋ∆÷––ƒѕт”“Ј≈іу£ђ«“µг![]() ѕт”“‘ЋґѓµƒЋўґ»ќ™√њ√л2Єцµ•ќї£ђ
ѕт”“‘ЋґѓµƒЋўґ»ќ™√њ√л2Єцµ•ќї£ђ ![]() Ј≈іуµƒЌђ ±Єя
Ј≈іуµƒЌђ ±Єя![]() “≤Ћж÷ЃЈ≈іу£ђµ±“‘
“≤Ћж÷ЃЈ≈іу£ђµ±“‘![]() ќ™÷±Њґµƒ‘≤”лґѓѕяґќ
ќ™÷±Њґµƒ‘≤”лґѓѕяґќ![]() Ћщ‘Џ÷±ѕяѕа«–£ђ«у
Ћщ‘Џ÷±ѕяѕа«–£ђ«у![]() µƒ÷µЇЌіЋ ±Cµгµƒ„ш±к.
µƒ÷µЇЌіЋ ±Cµгµƒ„ш±к.
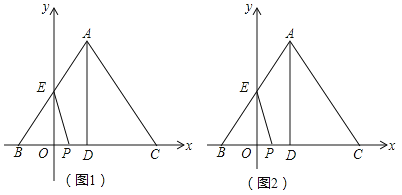
°Њір∞Є°њ(1)µг![]() µƒ„ш±кќ™(0,4);(2) t=
µƒ„ш±кќ™(0,4);(2) t=![]() їтt=1їтt=
їтt=1їтt=![]() £ї (3) µ±t=1 ±F”лґѓѕяґќADЋщ‘Џ÷±ѕяѕа«–,іЋ ±C(11,0).
£ї (3) µ±t=1 ±F”лґѓѕяґќADЋщ‘Џ÷±ѕяѕа«–,іЋ ±C(11,0).
°Њљвќц°њ ‘ћвЈ÷ќц£Ї ![]() „ѕ»«у≥ц÷±ѕяABµƒљвќц љ£ђ÷±љ”«уµ√
„ѕ»«у≥ц÷±ѕяABµƒљвќц љ£ђ÷±љ”«уµ√![]() µƒ„ш±к.
µƒ„ш±к.
£®2£©љшґшЈ÷±рјы”√Ґўµ±BE=BP ±£ђҐЏµ±EB=EP ±£ђҐџµ±PB=PE ±£ђµ√≥цtµƒ÷µЉіњ…£ї
£®3£© „ѕ»µ√≥ц![]() ‘ўјы”√‘Џ
‘ўјы”√‘Џ![]() ÷–£Ї
÷–£Ї ![]() £ђљшґш«у≥цtµƒ÷µ“‘Љ∞Cµг„ш±к£Ѓ
£ђљшґш«у≥цtµƒ÷µ“‘Љ∞Cµг„ш±к£Ѓ
‘ћвљвќц£Ї
.(1)°яAB=AC£ђAD°ЌBC£ђ
°аBD=CD=6£ђ
°яAB=10£ђ
°аAD=8£ђ
°аA(3,8)£ђ
…и÷±ѕяABµƒљвќц љќ™£Їy=kx+b,‘т![]() £ђ
£ђ
љвµ√£Ї 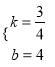 £ђ
£ђ
°а÷±ѕяABµƒљвќц љќ™£Їy=![]() x+4£ђ
x+4£ђ
°аE(0,4)£ђ
°аBE=5£ђ
(2)µ±°чBPE «µ»—ь»эљ«–ќ”–»э÷÷«йњц£Ї
Ґўµ±BE=BP ±,3+3t=5,љвµ√£Їt=![]() £ї
£ї
ҐЏµ±EB=EP ±£ђ3t=3£ђљвµ√£Їt=1£ї
Ґџµ±PB=PE ±£ђ
°яPB=PE£ђAB=AC£ђ°ѕABC=°ѕPBE£ђ
°а°ѕPEB=°ѕACB=°ѕABC£ђ
°а°чPBE°„°чABC£ђ
°а![]() £ђ
£ђ
°а![]() ,љвµ√£Їt=
,љвµ√£Їt=![]() £ђ
£ђ
„џ…ѕ£Їt=![]() їтt=1їтt=
їтt=1їтt=![]() £ї
£ї

(2)”…ћв“вµ√£ЇC(9+2t,0),
°аBC=12+2t£ђBD=CD=6+t£ђOD=3+t£ђ
…иFќ™EPµƒ÷–µг£ђЅђљ”OF£ђ„чFH°ЌAD£ђFG°ЌOP£ђ
°яFG°ќEO£ђ
°а°чPGF°„°чPOE£ђ
°аPG=OG=![]() t,FG=
t,FG=![]() EO=2,°аF(
EO=2,°аF(![]() t,2)£ђ
t,2)£ђ
°аFH=GD=ODOG=3+t![]() t=3
t=3![]() t£ђ
t£ђ
°яF”лґѓѕяґќADЋщ‘Џ÷±ѕяѕа«–,FH=12EP=3![]() t£ђ
t£ђ
‘ЏRt°чEOP÷–£Ї ![]()
°а4(3![]() t)=(3t)+16£ђ
t)=(3t)+16£ђ
љвµ√£Ї ![]() (…б»•)£ђ
(…б»•)£ђ
°аµ±t=1 ±F”лґѓѕяґќADЋщ‘Џ÷±ѕяѕа«–,іЋ ±C(11,0).