题目内容
【题目】在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.
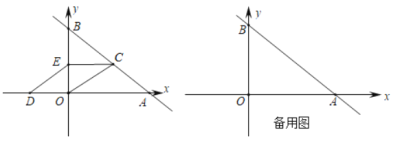
(1)k的值是 ;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求OCED的周长;
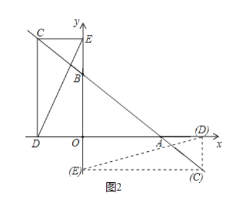
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为![]() ,请直接写出点C的坐标.
,请直接写出点C的坐标.
【答案】(1)![]() ;(2)①OCED的周长8+4
;(2)①OCED的周长8+4![]() ;②C的坐标为(﹣3,
;②C的坐标为(﹣3,![]() )或(11,
)或(11,![]() ).
).
【解析】
(1)根据点A的坐标,利用待定系数法可求出k值;
(2)①利用一次函数图象上点的坐标特征可得出点B的坐标,由平行四边形的性质结合点E为OB的中点可得出CE是△ABO的中位线,结合点A的坐标可得出CE的长,在Rt△DOE中,利用勾股定理可求出DE的长,再利用平行四边形的周长公式即可求出OCED的周长;
②设点C的坐标为(x,![]() ),则CE=|x|,CD=
),则CE=|x|,CD=![]() ,利用三角形的面积公式结合△CDE的面积为
,利用三角形的面积公式结合△CDE的面积为![]() 可得出关于x的方程,解之即可得出结论.
可得出关于x的方程,解之即可得出结论.
(1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:k=![]() .
.
故答案为:![]() .
.
(2)①由(1)可知直线AB的解析式为y=![]() x+4.
x+4.
当x=0时,y=![]() x+4=4,
x+4=4,
∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,
∴BE=OE=![]() OB=2.
OB=2.
∵点A的坐标为(8,0),
∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴![]() ,
,
∴BC=AC,
∴CE是△ABO的中位线,
∴CE=![]() OA=4.
OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE=![]() ,
,
∴C平行四边形OCED=2(OD+DE)=2(4+2![]() )=8+4
)=8+4![]() .
.
②设点C的坐标为(x,![]() +4),则CE=|x|,CD=|
+4),则CE=|x|,CD=|![]() x+4|,
x+4|,
∴S△CDE=![]() CDCE=|﹣
CDCE=|﹣![]() x2+2x|=
x2+2x|=![]() ,
,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3,![]() )或(11,
)或(11,![]() ).
).

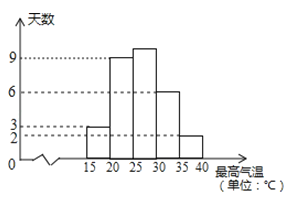
【题目】某甜品店计划订购一种鲜奶,根据以往的销售经验,当天的需求量与当天的最高气温![]() 有关,现将去年六月份(按30天计算)的有关情况统计如下:
有关,现将去年六月份(按30天计算)的有关情况统计如下:
(最高气温与需求量统计表)
最高气温 | 需求量(单位:杯) |
| 200 |
| 250 |
| 400 |
(1)求去年六月份最高气温不低于30℃的天数;
(2)若以最高气温位于各区间的频率估计最高气温位于该区间的概率,求去年六月份这种鲜奶一天的需求量不超过200杯的概率;
(3)若今年六月份每天的进货量均为350杯,每杯的进价为4元,售价为8元,未售出的这种鲜奶厂家以1元的价格收回销毁,假设今年与去年的情况大致一样,若今年六月份某天的最高气温![]() 满足
满足![]() (单位:℃),试估计这一天销售这种鲜奶所获得的利润为多少元?
(单位:℃),试估计这一天销售这种鲜奶所获得的利润为多少元?