题目内容
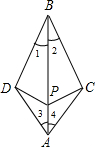已知如图，∠1=∠2，∠3=∠4，点P在AB上，可以得出PC=PD吗？为什么？
解：可得出PC=PD．
理由：∵∠1=∠2，∠3=∠4，AB=AB，
∴△ABD≌△ABC（ASA）．
∴AD=AC．
又∵PA=PA，
∴△ADP≌△ACP．
∴PC=PD．
分析：先利用ASA证明△ABD≌△ABC，得出AD=AC，再利用SAS证明△ADP≌△ACP，从而得出PC=PD．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
理由：∵∠1=∠2，∠3=∠4，AB=AB，
∴△ABD≌△ABC（ASA）．
∴AD=AC．
又∵PA=PA，
∴△ADP≌△ACP．
∴PC=PD．
分析：先利用ASA证明△ABD≌△ABC，得出AD=AC，再利用SAS证明△ADP≌△ACP，从而得出PC=PD．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
练习册系列答案
阅读快车系列答案
相关题目
过△ABC的三个顶点，已知如图，点C是线段AB的黄金分割点（AC＞BC），则下列结论中正确的是（ ）
| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．
已知如图，菱形ABCD中，∠ADC=120°，BD=2