题目内容
8.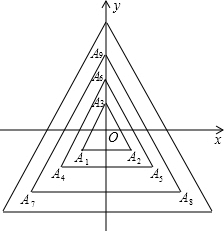 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2014的坐标是(-672,-672).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2014的坐标是(-672,-672).
分析 先根据每一个三角形有三个顶点确定出A2014所在的三角形,再求出相应的三角形的边长以及A2014的纵坐标的长度,即可得解.
解答 解:∵2014÷3=671…1,
∴A2014是第672个等边三角形的第1个顶点,
第672个等边三角形边长为2×672=1344,
∴点A2014的横坐标为 $\frac{1}{2}$×(-1344)=-672,
∵边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,
∴点A2014的纵坐标为-672,
∴点A2014的坐标为(-672,-672).
故答案为:(-672,-672).
点评 本题考查了点的坐标、等边三角形的性质,是点的变化规律,主要利用了等边三角形的性质,确定出点A2013和A2014所在三角形是解题的关键.

练习册系列答案
相关题目
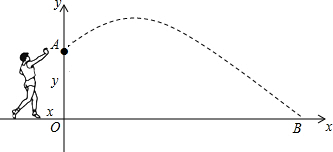 校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,求:
校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,求: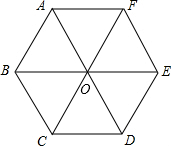 如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
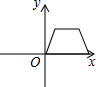
 如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm,AC与DG在同一直线上,开始时点A与点D重合,△ABC以1cm/s的速度向右移动,最终点A与点G重合,设重合部分(阴影部分)的面积为y(cm2),移动的时间为x(s).
如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm,AC与DG在同一直线上,开始时点A与点D重合,△ABC以1cm/s的速度向右移动,最终点A与点G重合,设重合部分(阴影部分)的面积为y(cm2),移动的时间为x(s).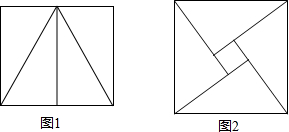 小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长
小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长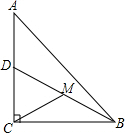 如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是1.5≤CM≤3.5.
如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是1.5≤CM≤3.5.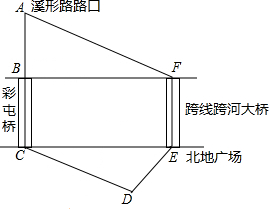 如图,家住彩屯溪形路路口的小李要经过彩屯到北地广场附近上班,路线为A→B→C→D→E.市政府决定修建设北地到彩屯的跨线跨河大桥EF,如果大桥建成后小李就可以由新大桥直线上班,路线A→F→E,BC∥EF,AB⊥BF,DE⊥CD,AB=420米,BC=300米,∠AFB=37°,∠CED=53°,请你帮助计算一下,小李改由新大桥上班会比原先少走多少米?(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,家住彩屯溪形路路口的小李要经过彩屯到北地广场附近上班,路线为A→B→C→D→E.市政府决定修建设北地到彩屯的跨线跨河大桥EF,如果大桥建成后小李就可以由新大桥直线上班,路线A→F→E,BC∥EF,AB⊥BF,DE⊥CD,AB=420米,BC=300米,∠AFB=37°,∠CED=53°,请你帮助计算一下,小李改由新大桥上班会比原先少走多少米?(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)