题目内容
 如图,AB是⊙O的直径,点C在⊙O上,
如图,AB是⊙O的直径,点C在⊙O上,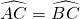 .动点P在弦BC上,则∠PAB可能为________度(写出一个符合条件的度数即可).
.动点P在弦BC上,则∠PAB可能为________度(写出一个符合条件的度数即可).
30
分析:首先连接OC,AC,由AB是⊙O的直径,点C在⊙O上,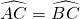 ,即可求得∠BOC的度数,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BAC的度数,继而可求得答案.
,即可求得∠BOC的度数,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BAC的度数,继而可求得答案.
解答: 解:连接OC,AC,
解:连接OC,AC,
∵AB是⊙O的直径,点C在⊙O上,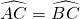 ,
,
∴∠BOC=90°,
∴∠BAC= ∠BOC=45°,
∠BOC=45°,
∵∠PAB<∠BAC,
∴∠PAB<45°.
∴∠PAB可能为30°.
此题答案不唯一,如30°.
故答案为:30.
点评:此题考查了圆周角定理与圆心角、弧的关系.此题难度不大,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用,注意掌握辅助线的作法.
分析:首先连接OC,AC,由AB是⊙O的直径,点C在⊙O上,
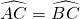 ,即可求得∠BOC的度数,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BAC的度数,继而可求得答案.
,即可求得∠BOC的度数,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BAC的度数,继而可求得答案.解答:
 解:连接OC,AC,
解:连接OC,AC,∵AB是⊙O的直径,点C在⊙O上,
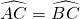 ,
,∴∠BOC=90°,
∴∠BAC=
 ∠BOC=45°,
∠BOC=45°,∵∠PAB<∠BAC,
∴∠PAB<45°.
∴∠PAB可能为30°.
此题答案不唯一,如30°.
故答案为:30.
点评:此题考查了圆周角定理与圆心角、弧的关系.此题难度不大,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用,注意掌握辅助线的作法.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为