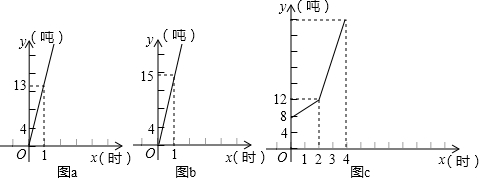
题目内容
17.为建设环境优美文明和谐的新农村,某村村委会决定在村道两旁种植A、B两种树木,需要购买两种树苗1000棵.已知购买一棵A品种树苗需花20元,购买一棵B品种树苗需花30元,另外每栽种一棵树苗需要植树费5元.设购买A品种树苗x棵,绿化村道的总费用为y元,解答下面问题(1)写出y与x的函数关系式;
(2)若绿化村道的总费用不超过31000元,则最多可购买B品种树苗多少棵?
(3)在(2)的条件下,由于A品种树苗成活率高,所以供应商把A品种树苗的单价上调了m(10≤m≤15)元,B品种树苗的单价不变,求出绿化总费用最低时的购买方案.
分析 (1)设购买A种树苗x棵,则购买B种树苗(1000-x)棵,根据总费用=(购买A种树苗的费用+种植A种树苗的费用)+(购买B种树苗的费用+种植B种树苗的费用),即可求出y(元)与x(棵)之间的函数关系式;
(2)根据绿化村道的总费用不超过31000元,列出关于x的一元一次不等式,求出x的取值范围,即可求解.
(3)根据总费用=种植A种树苗的总费用+种植B种树苗的总费用,即可求出y(元)与x(棵)之间的函数关系式y=(m-10)x+35000,根据m的取值和一次函数的性质进行判断即可.
解答 解:(1)y=(20+5)x+(30+5)(1000-x)=-10x+35000;
(2)-10x+35000≤31000,
解得:x≥400,
所以,最多可购买B种树苗600棵;
(3)y=(25+m)x+35(1000-x)
=(m-10)x+35000,
因为:10≤m≤15,所以当m=10时,无论怎样购买,绿化总费用都是35000元;
当10<m≤15,则m-10>0,所以y随x的减小而减小,所以取最小值400,y有最小值,所以购买方案是:A种树苗400棵,B种树苗600棵.
但无论怎样购买总费用均超过第(2)中的31000元,所以,按要求不能实现购买.
点评 此题考查了一次函数的应用,一元一次方程的应用,一元一次不等式的应用.此题难度适中,解题的关键是理解题意,根据题意求得函数解析式、列出方程与不等式,明确不等关系的语句“不超过”的含义.

练习册系列答案
相关题目
8.若代数式$\frac{2}{x-2}$和$\frac{2}{2x+1}$的值相等,则x=( )
| A. | 3 | B. | 7 | C. | -4 | D. | -3 |
12.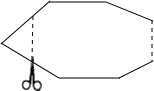 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )
 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
6.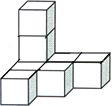 如图是由8个小正方体组合而成的几何体,它的俯视图是( )
如图是由8个小正方体组合而成的几何体,它的俯视图是( )
 如图是由8个小正方体组合而成的几何体,它的俯视图是( )
如图是由8个小正方体组合而成的几何体,它的俯视图是( )| A. | 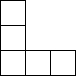 | B. | 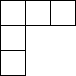 | C. |  | D. | 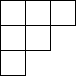 |