Question

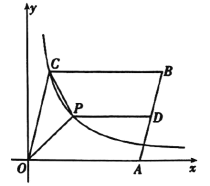
【题目】如图，在平面直角坐标系中，将一个图形绕原点顺时针方向旋转称为一次“直角旋转，已知的三个顶点的坐标分别为，，，完成下列任务：

（1）画出经过一次直角旋转后得到的；

（2）若点是内部的任意一点，将连续做次“直角旋转”（为正整数），点的对应点的坐标为，则的最小值为　　　；此时，与的位置关系为　　　．

(3)求出点旋转到点所经过的路径长．

Answer 1

【答案】（1）图见解析；（2）2，关于中心对称；（3）．

【解析】

（1）根据图形旋转的性质画出旋转后的△即可；

（2）根据中心对称的性质即可得出结论；

（3）根据弧长公式求解即可．

解：（1）如图，△即为所求；

（2）点的对应点的坐标为，

点与关于点对称，

．

故答案为：2，关于中心对称．

（3）∵点A坐标为

∴，

则旋转到点所经过的路径长．