Question

12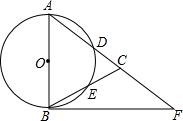．如图，在△ABC，AB=AC，以AB为直径的圆O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CAB=2∠CBF．
（1）求证：直线BF是圆O的切线；
（2）若AB=6，BF=8，求tan∠CBF；
（3）过点C作BF的平行线，交圆O于点M、N（M在N左边），交AB于点H，若AD=DC=4，CN=3，求∠CBF的任意一个三角函数．

Answer 1

分析 （1）连接AE．欲证BF是⊙O的切线，只需证明AB⊥BF即可；
（2）作辅助线CG（过点C作CG⊥BF于点G）构建平行线AB∥CG．由“平行线截线段成比例”知$\frac{FG}{BF}$=$\frac{FC}{AF}$=$\frac{4}{10}$=$\frac{2}{5}$，从而求得FG的值；然后根据图形中相关线段间的和差关系求得直角三角形CBG的两直角边BG、CG的长度；最后由锐角三角函数的定义来求tan∠CBF的值；
（3）根据已知证得△ABC是等边三角形，得出∠ABC=60°，进而求得∠CBF=30°，即可求得∠CBF的正弦函数．

解答 （1）证明：连接AE．
∵AB为⊙O的直径，
∴∠AEB=90°（直径所对的圆周角是直角），
∴∠BAE+∠ABE=90°（直角三角形的两个锐角互余）；
又∵AB=AC，AE⊥BC，
∴AE平分∠BAC，即∠BAE=∠CAE；
∵∠CAB=2∠CBF，
∴∠BAE=∠CBF，
∴∠BAE+∠ABE=∠ABE+∠CBF=90°，即AB⊥BF，
∵OB是半径，
∴BF为⊙O的切线；

（2）解：过点C作CG⊥BF于点G．
在Rt△ABF中，AB=6，BF=8，
∴AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=10；
又∵AC=AB=6
∴CF=4；
∵CG⊥BF，AB⊥BF，
∴CG∥AB，
∴$\frac{FG}{BF}$=$\frac{FC}{AF}$=$\frac{4}{10}$=$\frac{2}{5}$，
∴FG=$\frac{16}{5}$，
由勾股定理得：CG=$\sqrt{C{F}^{2}-F{G}^{2}}$=$\frac{12}{5}$，
∴BG=BF-FG=8-$\frac{16}{5}$=$\frac{24}{5}$，
在Rt△BCG中，tan∠CBF=$\frac{CG}{BG}$=$\frac{1}{2}$．

（3）解：连接BD，∵AB为⊙O的直径，
∴BD⊥AC，
∵AD=DC=4，
∴AB=BC，
∵AB=AC，
∴△ABC是等边三角形，
∴∠ABC=60°，
∵∠ABF=90°，
∴∠CBF=30°，
∴sin∠CBF=sin30°=$\frac{1}{2}$．

点评 本题是圆的综合题，考查了切线的判定与性质、勾股定理的应用、平行线截线段成比例、等腰三角形的判定和性质，等边三角形的判定和性质，解直角三角函数，圆周角定理等知识点．