题目内容
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
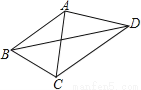
A. 68° B. 88° C. 90° D. 112°
B 【解析】试题分析:本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.根据等腰三角形两底角相等求出∠ABC=∠ACB,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD计算即可得解.如图,∵AB=AC=AD, ∴点B、C、D在以点A为圆心, 以AB的长为半径的圆上; ∵∠CBD=2∠BDC, ∠CAD=2∠CBD,∠BAC=2∠BDC, ∴∠CAD=...
练习册系列答案
相关题目
在“我为震灾献爱心”的捐赠活动中,某班40位同学捐款金额统计如下:
金额(元) | 20 | 30 | 35 | 50 | 100 |
学生数(人) | 3 | 7 | 5 | 15 | 10 |
则在这次活动中,该班同学捐款金额的众数和中位数是( )
A. 30,35 B. 50,35 C. 50,50 D. 15,50
C 【解析】捐款为50元的人数最多15人,故捐款金额的众数为50,将捐款金额按照有小到大的顺序排列为20、30、35、50、100,中间数据为35,故中位数为35.故选B已知一次函数y=ax+b(a、b为常数),x与y的部分对应值如下表:
x | –2 | –1 | 0 | 1 | 2 | 3 |
y | 6 | 4 | 2 | 0 | –2 | –4 |
那么方程ax+b=0的解是________,不等式ax+b>0的解集是_______.
x=1 x<1 【解析】(1). x=1 (2). x<1

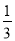 ,求DE的长.
,求DE的长.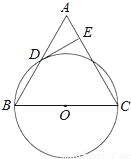
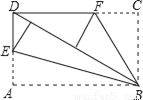
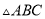 内接于⊙
内接于⊙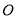 ,
, 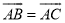 ,
, 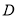 是
是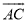 上一点(不与点
上一点(不与点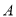 ,
, 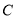 重合),延长
重合),延长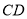 至点
至点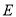 .
.
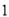 )求证:
)求证: 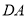 平分
平分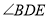 .
. )若
)若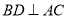 于点
于点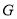 ,
, 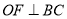 于点
于点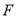 ,求证:
,求证: 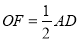 .
.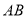 是⊙
是⊙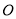 的直径,弦
的直径,弦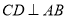 于
于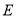 ,连接
,连接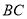 、
、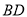 、
、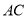 ,下列结论中不一定正确的是( ).
,下列结论中不一定正确的是( ).
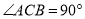 B.
B. 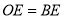 C.
C. 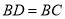 D. AD=AC
D. AD=AC