题目内容
8. 如图,在四边形ABCD中,∠ABC=90°,∠BAC=30°,BC=6,将四边形ABCD绕点A逆时针旋转30°至四边形AB′C′D′处,则旋转过程中,边BC所扫过的区域(图中阴影部分)的面积为3π.
如图,在四边形ABCD中,∠ABC=90°,∠BAC=30°,BC=6,将四边形ABCD绕点A逆时针旋转30°至四边形AB′C′D′处,则旋转过程中,边BC所扫过的区域(图中阴影部分)的面积为3π.
分析 先根据直角三角形的性质去除AN及AB的长,再由三角形的面积公式求出△ABC的面积,由扇形的面积公式得出扇形BAB′及扇形CAC′的面积,由S阴影=S1+S2即可得出结论.
解答 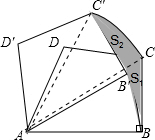 解:∵在四边形ABCD中,∠ABC=90°,BC=6,∠BAC=30°,
解:∵在四边形ABCD中,∠ABC=90°,BC=6,∠BAC=30°,
∴AC=12,AB=$\sqrt{{12}^{2}-{6}^{2}}$=6$\sqrt{3}$,S△ABC=$\frac{1}{2}$×6×6$\sqrt{3}$=18$\sqrt{3}$,
∴S扇形BAB′=$\frac{30}{360}$π×6($\sqrt{3}$)2=9π,
∴S1=18$\sqrt{3}$-9π.
∵S△AB′C′=S△ABC=18$\sqrt{3}$,S扇形CAC′=$\frac{30}{360}$π×122=12π,
∴S2=12π-18$\sqrt{3}$,
∴S阴影=S1+S2=18$\sqrt{3}$-9π+12π-18$\sqrt{3}$=3π.
故答案为:3π.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
3.用同样大小的黑色的小三角形按如图所示的规律摆放,则第100个图形有( )个黑色的小三角形.


| A. | 300 | B. | 303 | C. | 306 | D. | 309 |
20.随机抛掷一枚质地均匀的硬币两枚,两次都是正面朝上的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
18.下列方程中,有实数根的是( )
| A. | x2+1=0 | B. | x2+x+1=0 | C. | x2-x-1=0 | D. | x2-x+1=0 |
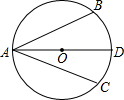 如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.
如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.