题目内容
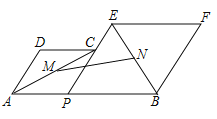
【题目】在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F，若AD＝
AB＝3，则S△ADF＝（ ）
A.2B.3
C.
D.
【答案】C
【解析】
由AD=
AB=3，可求得AB=，AD=3，又由在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F，根据轴对称的性质，可求得BE，CF的长，继而求得DF的长，于是求得答案．
解：∵AD＝AB＝3，
∴AB＝，AD＝3，
∵四边形ABCD是矩形，
∴BC＝AD＝3，CD＝AB＝，
∵在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F，
∴BE＝AB＝，
∴CF＝CE＝BC﹣BE＝3﹣，
∴DF＝CD﹣CF＝2﹣3，
∴S△ADF＝
ADDF＝×3×（2﹣3）＝3﹣
．
故选：C．
练习册系列答案
相关题目
【题目】某蔬菜市场为指导某种蔬菜的生产和销售，对往年的市场行情和生产情况进行了调查，提供的信息如下：
信息1：售价和月份满足一次函数关系，如下表所示．
月份 | … | 3 | 6 | … |
售价 | … | 5 | 3 | … |
信息2：成本和月份满足二次函数关系，并且知道该种蔬菜在6月成本达到最低为1元/千克，9月成本为4元/千克．
根据以上信息回答下列问题：
（1）在7月，这种蔬菜的成本是多少元每千克？
（2）在过去的一年中，某商家平均每天卖出
该种蔬菜，则哪个月的利润最大，最大利润为多少？（一个月按30天计算）
