题目内容
17.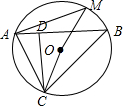 如图,△ABC内接于⊙O,CD⊥AB于D,求证:∠ACD=∠BCO.
如图,△ABC内接于⊙O,CD⊥AB于D,求证:∠ACD=∠BCO.
分析 延长CO交⊙O于M点,连结BM.根据同弧所对的圆周角相等得出∠CAB=∠CMB,由CM为⊙O的直径,根据直径所对的圆周角是直角得出∠CBM=90°,那么∠ADC=∠CBM=90°.然后根据三角形内角和定理得到∠CAD+∠ADC+∠ACD=180°,∠CMB+∠CBM+∠BCO=180°,利用等式的性质即可得出∠ACD=∠BCO.
解答 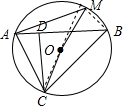 证明:延长CO交⊙O于M点,连结BM.则∠CAB=∠CMB.
证明:延长CO交⊙O于M点,连结BM.则∠CAB=∠CMB.
∵CM为⊙O的直径,
∴∠CBM=90°,
∴∠ADC=∠CBM=90°.
∵∠CAD+∠ADC+∠ACD=180°,
∠CMB+∠CBM+∠BCO=180°,
∴∠ACD=∠BCO.
点评 本题考查了圆周角定理,三角形内角和定理,等式的性质,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
相关题目
2.分式方程x-$\frac{5}{x-2}$=2-$\frac{5}{x-2}$的解的情况是( )
| A. | 只有一解x=2 | B. | 任意实数都是解 | C. | 无解 | D. | 解为x≠2 |
9.甲队修路120m与乙队修路100m所用天数相同,已知甲队比乙队每天多修10m,设乙队每天修路xm.依题意,下面所列方程正确的是( )
| A. | $\frac{120}{x}=\frac{100}{x-10}$ | B. | $\frac{120}{x+10}=\frac{100}{x}$ | C. | $\frac{120}{x-10}=\frac{100}{x}$ | D. | $\frac{120}{x}=\frac{100}{x+10}$ |
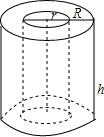 如图是一筒状的地膜示意图,其内圆半径和外圆半径分别为r=10厘米和R=20厘米,高h=50厘米.如果地膜的厚度是0.005厘米,你能计算出这些地膜的总长度是多少吗?
如图是一筒状的地膜示意图,其内圆半径和外圆半径分别为r=10厘米和R=20厘米,高h=50厘米.如果地膜的厚度是0.005厘米,你能计算出这些地膜的总长度是多少吗?