Question

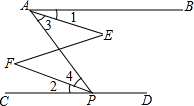如图，已知，∠BAP与∠APD互补，∠1=∠2，在_____中填上理由，说明∠E=∠F．
解：∵∠BAP+∠APD=180°

已知

∴AB∥CD

同旁内角互补，两直线平行

从而∠BAP=∠APC

两直线平行，内错角相等

又∠1=∠2

已知

∴∠BAP-∠1=∠APC-∠2

等式的性质

即∠3=∠4
∴AE∥PF（

内错角相等，两直线平行

）
则∠E=∠F（

两直线平行，内错角相等

）

Answer 1

分析：根据已知可得出AB∥CD，进而由∠1=∠2可证得∠3=∠4，故能得出AE∥FP，即能推出要证的结论成立．

解答：解：理由是：∵∠BAP+∠APD=180°（已知　　）
∴AB∥CD（同旁内角互补，两直线平行）
从而∠BAP=∠APC（两直线平行，内错角相等）
又∵∠1=∠2（已知）
∴∠BAP-∠1=∠APC-∠2（等式的性质）
即∠3=∠4
∴AE∥PF（内错角相等，两直线平行　）
∴∠E=∠F（两直线平行，内错角相等）
故答案为：已知，同旁内角互补，两直线平行，两直线平行，内错角相等，已知，等式的性质，内错角相等，两直线平行，两直线平行，内错角相等．

点评：本题考查了平行线的性质与判定，正确熟记平行线的判定和性质是解答本题的关键．