题目内容
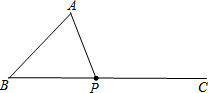 如图,已知∠B=45°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP=
如图,已知∠B=45°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP=| 2 |
| 2 |
| 2 |
| 2 |
分析:由于直角顶点不能确定,故应分∠APB=90°与∠BAP=90°两种情况进行分类讨论.
解答: 解:当∠APB=90°时,
解:当∠APB=90°时,
∵∠B=45°,AB=2cm,
∴BP1=AB•cos45°=2×
=
;
当∠BAP=90°时,
∵∠B=45°,AB=2cm,
∴BP2=
=
=2
.
故答案为:
或2
.
 解:当∠APB=90°时,
解:当∠APB=90°时,∵∠B=45°,AB=2cm,
∴BP1=AB•cos45°=2×
| ||
| 2 |
| 2 |
当∠BAP=90°时,
∵∠B=45°,AB=2cm,
∴BP2=
| AB |
| cos45° |
| 2 | ||||
|
| 2 |
故答案为:
| 2 |
| 2 |
点评:本题考查的是勾股定理的逆定理,在解答此题时要注意分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
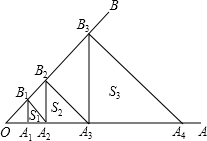 如图,已知∠AOB=45°,A1是OA上的一点,且OA1=1,过A1作OA的垂线交OB于点B1,过点B1作OB的垂线交OA于点A2,过点A2作OA的垂线交OB于点B2…,依次记△A1B1A2,△A2B2A3,△A3B3A4…的面积为S1,S2,S3…,则Sn=
如图,已知∠AOB=45°,A1是OA上的一点,且OA1=1,过A1作OA的垂线交OB于点B1,过点B1作OB的垂线交OA于点A2,过点A2作OA的垂线交OB于点B2…,依次记△A1B1A2,△A2B2A3,△A3B3A4…的面积为S1,S2,S3…,则Sn= (2013•铜仁地区)如图,已知∠AOB=45°,A1、A2、A3、…在射线OA上,B1、B2、B3、…在射线OB上,且A1B1⊥OA,A2B2⊥OA,…AnBn⊥OA;A2B1⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6…).若OA1=1,则A6B6的长是
(2013•铜仁地区)如图,已知∠AOB=45°,A1、A2、A3、…在射线OA上,B1、B2、B3、…在射线OB上,且A1B1⊥OA,A2B2⊥OA,…AnBn⊥OA;A2B1⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6…).若OA1=1,则A6B6的长是 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=
 如图,已知∠AOB=45°,过OA上的点A1,A2,A3,A4,…分别作OA的垂线,与OB交于点B1,B2,B3,B4,…,OA1=A1A2=A2A3=A3A4=…,设梯形A1A2B2B1的面积为S1,梯形A3A4B4B3的面积为S2,梯形A5A6B6B5的面积为S3,…,若S1=6,则S10=
如图,已知∠AOB=45°,过OA上的点A1,A2,A3,A4,…分别作OA的垂线,与OB交于点B1,B2,B3,B4,…,OA1=A1A2=A2A3=A3A4=…,设梯形A1A2B2B1的面积为S1,梯形A3A4B4B3的面积为S2,梯形A5A6B6B5的面积为S3,…,若S1=6,则S10=