题目内容
11. 如图,已知正比例函数图象经过点A(2,3),B(m,6).
如图,已知正比例函数图象经过点A(2,3),B(m,6).(1)求正比例函数的解析式及m的值.
(2)分别过点A与点B作y轴的平行线,与反比例函数在第一象限内的分支分别交于点C、D(点C、D均在点A、B下方),若BD=5AC,求反比例函数的解析式.
分析 (1)设正比例函数的解析式为y=kx,代入A的坐标根据待定系数法即可求得正比例函数的解析式,把B代入即可求得m的值;
(2)根据题意得出C点的横坐标为2,D点的横坐标为4,设反比例函数的解析式为y=$\frac{m}{x}$,分别代入得yC=$\frac{m}{2}$,yD=$\frac{m}{4}$,进而求得AC=3-$\frac{m}{2}$,BD=6-$\frac{m}{4}$,根据BD=5AC列出5(3-$\frac{m}{2}$)=6-$\frac{m}{4}$,解方程求得m的值,即可求得解析式.
解答 解:(1)设正比例函数的解析式为y=kx,
∵正比例函数图象经过点A(2,3),
∴3=2k,
∴k=$\frac{3}{2}$,
∴比例函数的解析式为y=$\frac{3}{2}$x;
把B(m,6)代入解析式得,6=$\frac{3}{2}$m,
解得m=4;
(2)∵AC∥BD∥y轴,
∴C点的横坐标为2,D点的横坐标为4,
设反比例函数的解析式为y=$\frac{m}{x}$,分别代入得yC=$\frac{m}{2}$,yD=$\frac{m}{4}$,
∴AC=3-$\frac{m}{2}$,BD=6-$\frac{m}{4}$,
∵BD=5AC,
∴BD=5AC,
∴5(3-$\frac{m}{2}$)=6-$\frac{m}{4}$,
解得m=4,
∴反比例函数的解析式为y=$\frac{4}{x}$.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求反比例函数和一次函数的解析式,根据题意求得C、D的坐标是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
 如图,BD为△ABC的角平分线,∠BAC=2∠C,GE⊥BD于F,交BC于E,探究线段AD、AG、EC间的数量关系.
如图,BD为△ABC的角平分线,∠BAC=2∠C,GE⊥BD于F,交BC于E,探究线段AD、AG、EC间的数量关系. 如图,抛物线y=(x+2)2-9与x轴交于点A、B(点A在点B的左边).
如图,抛物线y=(x+2)2-9与x轴交于点A、B(点A在点B的左边). 某空军加油飞机给另一架正在飞行的运输飞机进行空中加油,在加油的过程中,设运输飞机的油箱余油量为y1(吨).加油飞机的油箱余油量为y2(吨),已知y1(吨),y2(吨)与加油时间t(分)之间的函数关系图象如图所示.
某空军加油飞机给另一架正在飞行的运输飞机进行空中加油,在加油的过程中,设运输飞机的油箱余油量为y1(吨).加油飞机的油箱余油量为y2(吨),已知y1(吨),y2(吨)与加油时间t(分)之间的函数关系图象如图所示. 如图,AD是△ABC的高,四边形PQRS是矩形,且点P、Q在BC边上,点R在AC边上,点S在AB边上,矩形的长是宽的2倍,其中BC=30cm,AD=20cm.
如图,AD是△ABC的高,四边形PQRS是矩形,且点P、Q在BC边上,点R在AC边上,点S在AB边上,矩形的长是宽的2倍,其中BC=30cm,AD=20cm.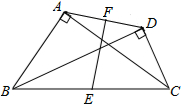 已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD.
已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD.