题目内容
如图，AD=AE，BE=CD，∠ADB=∠AEC=110°，∠BAE=70°，则∠CAE=（ ）分析：运用SAS证明△ABD≌△ACE，得∠BAD=∠CAE．根据三角形内角和定理可求∠DAE的度数．则易求∠CAE的度数．
解答：
解：如图，∵∠1=∠2=110°，
∴∠ADE=∠AED=70°，
∴∠DAE=180°-2×70°=40°．
∵BE=CD，
∴BD=CE．
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS）
∴∠BAD=∠CAE．
∵∠BAE=70°，
∴∠BAD=∠CAE=30°．
故选B．
解：如图，∵∠1=∠2=110°，∴∠ADE=∠AED=70°，
∴∠DAE=180°-2×70°=40°．
∵BE=CD，
∴BD=CE．
在△ABD和△ACE中，
|
∴△ABD≌△ACE（SAS）
∴∠BAD=∠CAE．
∵∠BAE=70°，
∴∠BAD=∠CAE=30°．
故选B．
点评：此题考查等腰三角形的判定和性质及三角形内角和定理，证明三角形为等腰三角形是关键．
练习册系列答案
相关题目
2、如图，AD=AE，∠1=∠2，BD=CE，则有△ABD≌△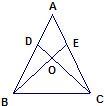
21、已知：如图，AD=AE，∠ADC=∠AEB，BE与CD相交于O点．
39、已知：如图，AD=AE，AB=AC，BD、CE相交于O．
23、已知：如图，AD=AE，AB=AC，DC与BE交于O点．
如图，AD=AE，AB=AC，∠A=60°，∠C=25°，则∠DOB=