题目内容
1.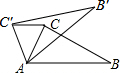 如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )| A. | 40° | B. | 50° | C. | 30° | D. | 35° |
分析 先根据平行线的性质得∠ACC′=∠CAB=70°,再根据旋转得性质得AC=AC′,∠CAC′等于旋转角,然后利用等腰三角形的性质和三角形内角和计算出∠CAC′的度数即可.
解答 解:∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∵△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,
∴AC=AC′,∠CAC′等于旋转角,
∴∠AC′C=∠ACC′=70°,
∴∠CAC′=180°-70°-70°=40°,
∴旋转角α的度数为40°.
故选A.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知线段a,求作:边长为a的正四边形,正六边形.
已知线段a,求作:边长为a的正四边形,正六边形.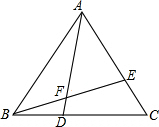 如图,已知在等边△ABC中,点D、E分别在BC,AC上,BD=CE,AD与BE交于点F
如图,已知在等边△ABC中,点D、E分别在BC,AC上,BD=CE,AD与BE交于点F