题目内容
4.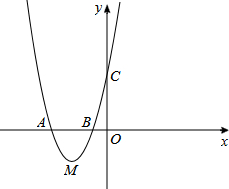 如图,抛物线经过A(-2,0),B(-$\frac{1}{2}$,0),C(0,2)三点.
如图,抛物线经过A(-2,0),B(-$\frac{1}{2}$,0),C(0,2)三点.(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足∠AMH=90°?若存在,请求出点H的坐标;若不存在,请说明理由.
分析 (1)根据待定系数法,可得抛物线的解析式;
(2)根据图形的割补法,可得面积的和差,根据二次函数的性质,可得答案;
(3)根据余角的性质,可得∠AMN=∠NKM,根据相似三角形的判定与性质,可得$\frac{AN}{MN}$=$\frac{MN}{NK}$,根据解方程组,可得H点坐标.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,将A(-2,0),B(-$\frac{1}{2}$,0),C(0,2)代入解析式,得
$\left\{\begin{array}{l}{4a-2b+c=0}\\{\frac{1}{4}a-\frac{1}{2}b+c=0}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=5}\\{c=2}\end{array}\right.$.
∴抛物线的解析式是y=2x2+5x+2;
(2)由题意可求得AC的解析式为y=x+2,
如图1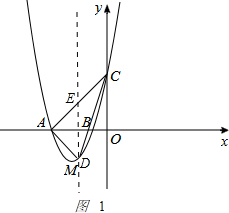 ,
,
设D点的坐标为(t,2t2+5t+2),过D作DE⊥x轴交AC于E点,
∴E点的坐标为(t,t+2),
DE=t+2-(2t2+5t+2)=-2t2-4t,用h表示点C到线段DE所在直线的距离,
S△DAC=S△CDE+S△ADE=$\frac{1}{2}$DE•h+$\frac{1}{2}$DE(2-h)=$\frac{1}{2}$DE•2=DE=-2t2-4t=-2(t+1)2+2
∵-2<t<0,
∴当t=-1时,△DCA的面积最大,此时D点的坐标为(-1,-1);
(3)存在点H满足∠AMH=90°,
由(1)知M点的坐标为(-$\frac{5}{4}$,-$\frac{9}{8}$)
如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N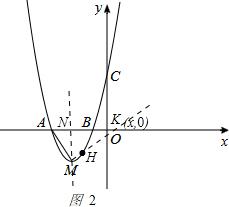 ,
,
∵∠AMN+∠KMN=90°,∠NKM+∠KMN=90°,
∴∠AMN=∠NKM.
∵∠ANM=∠MNK,
∴△AMN∽△MKN,
∴$\frac{AN}{MN}$=$\frac{MN}{NK}$,
∴MN2=AN•NK,
∴($\frac{9}{8}$)2=(2-$\frac{5}{4}$)(x+$\frac{5}{4}$),
解得x=$\frac{7}{16}$
∴K点坐标为($\frac{7}{16}$,0)
直线MK的解析式为y=$\frac{2}{3}$x-$\frac{7}{24}$,
∴$\left\{\begin{array}{l}{y=\frac{2}{3}x-\frac{7}{24}①}\\{y=2{x}^{2}+5x+2②}\end{array}\right.$,
把①代入②,化简得48x2+104x+55=0.
△=1042-4×48×55=64×4=256>0,
∴x1=-$\frac{5}{4}$,x2=-$\frac{11}{12}$,将x2=-$\frac{11}{12}$代入y=$\frac{2}{3}$x-$\frac{7}{24}$,
解得y=-$\frac{65}{72}$
∴直线MN与抛物线有两个交点M、H,
∴抛物线上存在点H,满足∠AMH=90°,
此时点H的坐标为(-$\frac{11}{12}$,-$\frac{65}{72}$).
点评 本题考察了二次函数综合题,(1)利用待定系数法求函数解析式;(2)利用图形割补法求面积是解题关键,(3)利用相似三角形的判定与性质得出$\frac{AN}{MN}$=$\frac{MN}{NK}$是解题关键,解方程组是此题的难点.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| x | -4.1 | -4.2 | -4.3 | -4.4 |
| x2+2x-k | -1.39 | -0.76 | -0.11 | 0.56 |
| A. | -4.1 | B. | -4.2 | C. | -4.3 | D. | -4.4 |
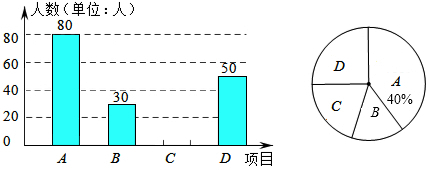
| A. | 240 | B. | 120 | C. | 80 | D. | 40 |
| A. | -1<x<2 | B. | 1<x≤2 | C. | -1<x≤2 | D. | -1<x≤3 |
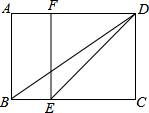 已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.
已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD. 正方形A1B1C1O和A2B2C2C1按如图所示方式放置,点A1,A2在直线y=x+1上,点C1,C2在x轴上.已知A1点的坐标是(0,1),则点B2的坐标为(3,2).
正方形A1B1C1O和A2B2C2C1按如图所示方式放置,点A1,A2在直线y=x+1上,点C1,C2在x轴上.已知A1点的坐标是(0,1),则点B2的坐标为(3,2).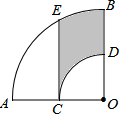 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点O为圆心,OC的长为半径作$\widehat{CD}$交OB于点D.若OA=2,则阴影部分的面积为$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点O为圆心,OC的长为半径作$\widehat{CD}$交OB于点D.若OA=2,则阴影部分的面积为$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.