题目内容
11．
如图，矩形ABCD中，AB=2，将矩形ABCD绕点D逆时针旋转90°，点A、C分别落在点A′、C′处，如果点A′、C′、B在同一条直线上，那么tan∠CBA′的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{5}-1}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{2\sqrt{5}-1}{4}$ |
分析 如图，连接B、A′、C′，由题意可知∠CBA′=∠AC′D，可设AD=x，则可知A′D=x，A′C=2-x，在Rt△CBA′和Rt△A′C′D中，利用正切函数的定义可得关于x的方程，可求得x的值，再由正切函数的定义可求得答案．
解答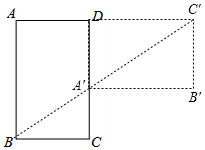 
解：
∵四边形ABCD为矩形，
∴AB=CD=2，
由旋转的性质可得AD=AD′，C′D=AB=2，
设AD=x，则A′D=x，A′C=2-x，
∵A′、C′、B在同一条直线上，且A′B′∥C′D，
∴∠CBA′=∠DC′A′，
∴tan∠CBA′=tan∠DC′A′，
即$\frac{x}{2}$=$\frac{2-x}{x}$，解得x=-1+$\sqrt{5}$或x=-1-$\sqrt{5}$（小于0，不合题意，舍去），
∴tanCBA′=$\frac{x}{2}$=$\frac{\sqrt{5}-1}{2}$，
故选B．
点评 本题主要考查矩形的性质、旋转的性质及三角函数的定义，利用旋转的性质和正切函数的定义求得矩形的宽是解题的关键．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
19．某原料仓库一天的原料进出记录如表（运进用正数表示，运出用负数表示）：
（1）这天仓库的原料比原来增加了还是减少？请说明理由；
（2）根据实际情况，现有两种方案：
方案一：运进每吨原料费用6元，运出每吨费用9元；
方案二：不管运进还是运出费用都是每吨原料7元．从节约运费的角度考虑，选用哪一种方案较合适．
（3）在（2）的条件下，设运进原料共x吨，运出原料共y吨，x、y满足什么关系时，两种方案的运费相同．
| 进出数量（t） | -4 | 5 | -2 | 3 | -3 |
| 进出次数 | 1 | 2 | 4 | 4 | 3 |
（2）根据实际情况，现有两种方案：
方案一：运进每吨原料费用6元，运出每吨费用9元；
方案二：不管运进还是运出费用都是每吨原料7元．从节约运费的角度考虑，选用哪一种方案较合适．
（3）在（2）的条件下，设运进原料共x吨，运出原料共y吨，x、y满足什么关系时，两种方案的运费相同．
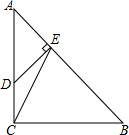如图，在Rt△ABC中，∠ACB=90°，AC=BC=3，点D在边AC上，且AD=2CD，DE⊥AB，垂足为点E，联结CE．求：