题目内容
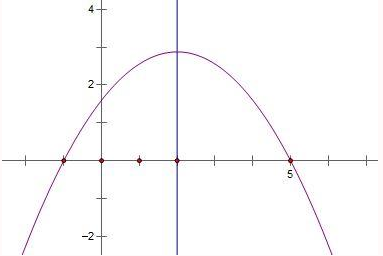 已知y=ax2+bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:
已知y=ax2+bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:(1)4a+b=0;(2)c+9a>3b;(3)8a+7b+2c<0.
正确结论有几个?
考点:二次函数图象与系数的关系
专题:
分析:(1)利用抛物线的对称轴即可判定;
(2)把x=-3时代入即可判定;
(3)由抛物线与x的交点为(-1,0),可得a-b+c=0,由b=-4a,可得c=-5a,化简8a+7b+2c=8a-28a-10a=-30a,由a<0,即可得8a+7b+2c>0.
(2)把x=-3时代入即可判定;
(3)由抛物线与x的交点为(-1,0),可得a-b+c=0,由b=-4a,可得c=-5a,化简8a+7b+2c=8a-28a-10a=-30a,由a<0,即可得8a+7b+2c>0.
解答:解:(1)∵抛物线的对称轴为x=-
=2,
∴b=-4a,即4a+b=0,所以①正确.
(2)∵当x=-3时,y<0,
∴9a-3b+c<0,即c+9a<3b.
∴②错误.
(3)∵抛物线与x的交点为(-1,0),
∴a-b+c=0,
∵b=-4a,
a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
∵a<0,
∴8a+7b+2c>0.
∴③错误.
所以正确的有1个.
| b |
| 2a |
∴b=-4a,即4a+b=0,所以①正确.
(2)∵当x=-3时,y<0,
∴9a-3b+c<0,即c+9a<3b.
∴②错误.
(3)∵抛物线与x的交点为(-1,0),
∴a-b+c=0,
∵b=-4a,
a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
∵a<0,
∴8a+7b+2c>0.
∴③错误.
所以正确的有1个.
点评:本题主要考查了二次函数图象与系数关系,解题的关键是利用对称轴求出a,b的关系.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列概念表述正确的是( )
| A、单项式ab的系数是0,次数是2 | ||
| B、-2πx2y3的系数是-2,次数是6 | ||
C、
| ||
| D、-ab2+3a-1的项是-ab2、3a、1 |