题目内容
3.甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别搅匀两箱中的球后,从这两箱中分别任意摸出一个球.正确说法是( )| A. | 从甲、乙两箱摸到黑球的概率相等 | |
| B. | 从甲箱摸到黑球的概率较大 | |
| C. | 从乙箱摸到黑球的概率较大 | |
| D. | 无法比较从甲、乙两箱摸到黑球的概率 |
分析 根据随机事件概率大小的求法,找准两点:①各箱中符合条件的黑球数目;②各箱中球的总数.二者的比值就是其发生的概率的大小,算出相应概率后比较即可.
解答 解:∵甲箱装有40个红球和10个黑球,
球的总个数为:40+10=50个;
黑球的个数为:10个,
∵乙箱装有60个红球、40个黑球和50个白球,
球的总个数为:60+40+50=150个,
黑球的个数为:40个,
于是:从甲箱摸到黑球的概率$\frac{10}{50}$=$\frac{1}{5}$;
从乙箱摸到黑球的概率$\frac{40}{150}$=$\frac{4}{15}$;
由此可得从乙箱摸到黑球的概率较大,
故选:C.
点评 本题考查概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
18.二次函数y=-2(x-3)2+1的图象的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=-3 | C. | 直线x=3 | D. | 直线x=1 |
15.关于正比例函数y=-2x,下列说法正确的是( )
| A. | y随x的增大而增大 | |
| B. | 图象是经过第一、第二象限的一条直线 | |
| C. | 图象向上平移1个单位长度后得到直线y=-2x+1 | |
| D. | 点(1,2)在其图象上 |
13. 实施新课程改革以来,某校开设了综合实践课,为了了解同学们对该课程的看法,对400名同学作了问卷调查,并将调查结果绘制成如图的扇形统计图.
实施新课程改革以来,某校开设了综合实践课,为了了解同学们对该课程的看法,对400名同学作了问卷调查,并将调查结果绘制成如图的扇形统计图.
(1)分别计算出持每一种意见的确定人数,填写在下表中.
(2)从扇形统计图与统计数据中你能得出什么结论?说说你的理由.
 实施新课程改革以来,某校开设了综合实践课,为了了解同学们对该课程的看法,对400名同学作了问卷调查,并将调查结果绘制成如图的扇形统计图.
实施新课程改革以来,某校开设了综合实践课,为了了解同学们对该课程的看法,对400名同学作了问卷调查,并将调查结果绘制成如图的扇形统计图.(1)分别计算出持每一种意见的确定人数,填写在下表中.
| 意见 | 非常喜欢 | 喜欢 | 有一点喜欢 | 不喜欢 |
| 人数 |
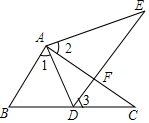 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证: 如图,是每个面上都标有一个汉字的正方体的平面展开图,在此正方体上与“江”字相对的面上的汉字是城.
如图,是每个面上都标有一个汉字的正方体的平面展开图,在此正方体上与“江”字相对的面上的汉字是城.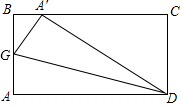 如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度.
如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度. 已知:如图∠B=40°,∠B=∠BAD,∠C=∠ADC,则∠DAC的度数为20°.
已知:如图∠B=40°,∠B=∠BAD,∠C=∠ADC,则∠DAC的度数为20°.