题目内容
已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点.
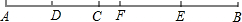
(1)如图,若AC=4,BC=6,求CF的长;
(2)若AB=16CF,求
的值;
(3)若AC>BC,AC-BC=a,取DC的中点D1,CE的中点E1,D1E1的中点F1,则CF1= .(用含a的代数式表示)
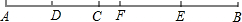
(1)如图,若AC=4,BC=6,求CF的长;
(2)若AB=16CF,求
| AC |
| CB |
(3)若AC>BC,AC-BC=a,取DC的中点D1,CE的中点E1,D1E1的中点F1,则CF1=
考点:两点间的距离
专题:计算题
分析:(1)由D为AC的中点,E为BC的中点得到DC=
AC=2,CE=
BC=3,则可计算出DE=5,再利用F为DE的中点得到DF=
DE=
,然后利用CF=DF-DC求解;
(2)设AC=x,BC=y,易得DE=DC+CE=
(x+y),再计算出DF=
DE=
(x+y),所以CF=DF-DC=
(y-x),接着利用AB=16CF得到x+y=16•
(y-x),化简后有5x=3y,然后利用比例性质即可得到
的值;
(3)如图,设AC=x,BC=y,即x-y=a,利用线段中点定义得到DC=
x,CE=
y,则D1C=
x,CE1=
y,所以D1E1=
(x+y),再利用D1E1的中点为F1得到D1F1=
D1E1=
(x+y),于是可计算出F1C=D1C-D1F1=
(x-y),即有F1C=
a.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
(2)设AC=x,BC=y,易得DE=DC+CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| AC |
| CB |
(3)如图,设AC=x,BC=y,即x-y=a,利用线段中点定义得到DC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
解答:解:(1)∵D为AC的中点,E为BC的中点,
∴DC=
AC=2,CE=
BC=3,
∴DE=DC+CE=2+3=5,
∵F为DE的中点,
∴DF=
DE=
,
∴CF=DF-DC=
-2=
;
(2)设AC=x,BC=y,则DC=
AC=
x,CE=
BC=
y,
∴DE=DC+CE=
(x+y),
∵F为DE的中点,
∴DF=
DE=
(x+y),
∴CF=DF-DC=
(x+y)-
x=
(y-x);
∵AB=16CF,
∴x+y=16•
(y-x),
∴5x=3y,
∴
=
,
即
的值为
;
(3)如图,
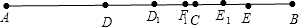
设AC=x,BC=y,即x-y=a,则DC=
AC=
x,CE=
BC=
y,
∵DC的中点为D1,CE的中点为E1,
∴D1C=
CD=
x,CE1=
CE=
y,
∴D1E1=
(x+y),
∵D1E1的中点为F1,
∴D1F1=
D1E1=
(x+y),
∴F1C=D1C-D1F1=
x-
(x+y)=
(x-y),
∴F1C=
a.
故答案为
a
∴DC=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=DC+CE=2+3=5,
∵F为DE的中点,
∴DF=
| 1 |
| 2 |
| 5 |
| 2 |
∴CF=DF-DC=
| 5 |
| 2 |
| 1 |
| 2 |
(2)设AC=x,BC=y,则DC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=DC+CE=
| 1 |
| 2 |
∵F为DE的中点,
∴DF=
| 1 |
| 2 |
| 1 |
| 4 |
∴CF=DF-DC=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∵AB=16CF,
∴x+y=16•
| 1 |
| 4 |
∴5x=3y,
∴
| x |
| y |
| 3 |
| 5 |
即
| AC |
| CB |
| 3 |
| 5 |
(3)如图,
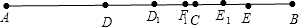
设AC=x,BC=y,即x-y=a,则DC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵DC的中点为D1,CE的中点为E1,
∴D1C=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴D1E1=
| 1 |
| 4 |
∵D1E1的中点为F1,
∴D1F1=
| 1 |
| 2 |
| 1 |
| 8 |
∴F1C=D1C-D1F1=
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
∴F1C=
| 1 |
| 8 |
故答案为
| 1 |
| 8 |
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.理清线段之间的关系是解决本题的关键.

练习册系列答案
相关题目
下列算式中正确的有( )
0-3
=3
;0-(-
)=
;(+
)-0=
;(-
)+0=
.
0-3
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
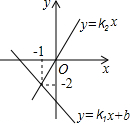 同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )| A、x=0 | B、x=-1 |
| C、x=-2 | D、x=1 |
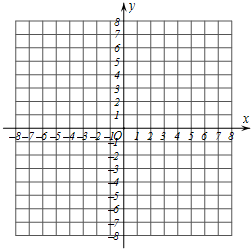 已知,△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).
已知,△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).
 如图,正方形ABCD各顶点均在正方形EFGH的各边上(GB<BF),且两正方形面积分别为25和49,则tan∠ABF=
如图,正方形ABCD各顶点均在正方形EFGH的各边上(GB<BF),且两正方形面积分别为25和49,则tan∠ABF= 我国网球名将李娜在今年法国网球公开赛上的出色表现,大大激发了国人对网球的热情.在一项“你最喜欢的球类运动”的调查中,共有50名同学参与调查,每人必选且只选一项,将调查结果绘制成频数分布直方图如下,根据图中信息回答:
我国网球名将李娜在今年法国网球公开赛上的出色表现,大大激发了国人对网球的热情.在一项“你最喜欢的球类运动”的调查中,共有50名同学参与调查,每人必选且只选一项,将调查结果绘制成频数分布直方图如下,根据图中信息回答: