题目内容
设e=
，c2-5ac+6a2=0，则e=
| c | a |
2或3
2或3
．分析：根据题意，将等式c2-5ac+6a2=0两边同时除以a2，得出关于e的一元二次方程，求解即可．
解答：解：∵c2-5ac+6a2=0，
∴（c2-5ac+6a2）÷a2=0，
即（
）2-5×
+6=0，
∵e=
，
∴e2-5e+6=0
因式分解得，（e-2）（e-3）=0，
解得e=2或3．
故答案为2或3．
∴（c2-5ac+6a2）÷a2=0，
即（
| c |
| a |
| c |
| a |
∵e=
| c |
| a |
∴e2-5e+6=0
因式分解得，（e-2）（e-3）=0，
解得e=2或3．
故答案为2或3．
点评：本题考查了用因式分解法解一元二次方程，解题的关键是将原等式转化成关于e的一元二次方程．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
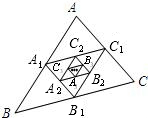如图，已知△ABC的周长为m，分别连接AB，BC，CA的中点A1，B1，C1得△A1B1C1，再连接A1B1，B1C1，C1A1的中点A2，B2，C2得△A2B2C2，再连接A2B2，B2C2，C2A2的中点A3，B3，C3得△A3B3C3，…，这样延续下去，最后得△AnBnCn．设△A1B1C1的周长为l1，△A2B2C2的周长为l2，△A3B3C3的周长为l3，…，△AnBnCn的周长为ln，则ln=设H为锐角△ABC的三条高AD、BE、CF的交点，若BC=a，AC=b，AB=c，则AH•AD+BH•BE+CH•CF等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|