题目内容
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足 =
= ,
,
过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
(1)求证:AE⊥DE;
(2)若tan∠CBA=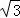 ,AE=3,求AF的长.
,AE=3,求AF的长.
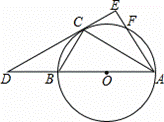
(1)证明:连接OC,
∵OC=OA,
∴∠BAC=∠OCA,
 ∵
∵ =
= ,
,
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE, 3分
∵DE切⊙O于点C,
∴OC⊥DE,
∴AE⊥DE; 6分
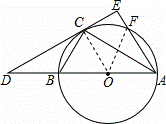
(2)解:∵AB是⊙O的直径,
∴△ABC是直角三角形,
∵tan∠CBA= ,
,
∴∠CBA=60°,
∴∠BAC=∠EAC=30°,
∵△AEC为直角三角形,AE=3,
∴AC=2 ,
,  9分
9分
连接OF,
∵OF=OA,∠OAF=∠BAC+∠EAC=60°,
∴△OAF为等边三角形,
∴AF=OA=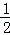 AB,
AB,
 在Rt△ACB中,AC=2
在Rt△ACB中,AC=2 ,tan∠CBA=
,tan∠CBA= ,
,
∴BC=2,(直接给出AF=2不扣分)
∴AB=4,
∴AF=2. 12分

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案



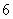 的平方根是
的平方根是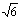
 ; ②
; ②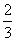 π;是真命题的概率是 .
π;是真命题的概率是 .  平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函
平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.





 =
=