题目内容
20．若$\frac{m-3}{m-1}$•|m|=$\frac{m-3}{m-1}$，则m=3或-1．分析 利用绝对值和分式的性质可得m-1≠0，m-3=0或|m|=1，可得m．
解答 解：由题意得，
m-1≠0，
则m≠1，
（m-3）•|m|=m-3，
∴（m-3）•（|m|-1）=0，
∴m=3或m=±1，
∵m≠1，
∴m=3或m=-1，
故答案为：3或-1．
点评 本题主要考查了绝对值和分式的性质，熟记分式分母不为0是解答此题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，已知△ABC，∠B=40°．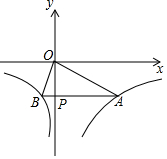
已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}（{x＞0}）\\ \frac{3}{x}（{x＜0}）\end{array}$的图象如图所示，点P是y轴负半轴上一动点，过点P作y轴的垂线交图象于A，B两点，连接OA、OB．下列结论：
8．
如图，将一块三角板的45°顶点放在直尺的一边上，当∠1=63°时，∠2=（ ）
如图，将一块三角板的45°顶点放在直尺的一边上，当∠1=63°时，∠2=（ ）| A． | 108° | B． | 72° | C． | 77° | D． | 82° |
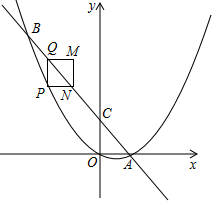抛物线y=ax2+bx与直线y=mx+n交于点A（1，0），B（-2，6），点P是直线AB下方抛物线上的一个动点．
12．我们知道方程x2+2x-3=0的解是x1=1，x2=-3，现给出另一个方程（2x+3）2+2（2x+3）-3=0，它的解是（ ）
| A． | x1=1，x2=3 | B． | x1=1，x2=-3 | C． | x1=-1，x2=3 | D． | x1=-1，x2=-3 |
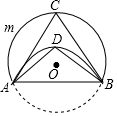如图，将⊙O沿弦AB折叠，点C在$\widehat{AmB}$上，点D在$\widehat{AB}$上，若∠ACB=70°，则∠ADB=110°．