题目内容
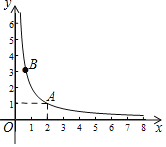
【题目】如图,在平面直角坐标系![]() 中的第一象限内,反比例函数图象过点
中的第一象限内,反比例函数图象过点![]() 和另一动点
和另一动点![]() .
.
(1)求此函数表达式;
(2)如果![]() ,写出
,写出![]() 的取值范围;
的取值范围;
(3)直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,如果
,如果![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为(0,3)或(6,0).
的坐标为(0,3)或(6,0).
【解析】
(1)由点![]() 的坐标,利用待定系数法即可求出反比例函数表达式;
的坐标,利用待定系数法即可求出反比例函数表达式;
(2)求![]() 时x的取值范围就是求A点上方的函数图象对应的x的取值范围,据图写出即可;
时x的取值范围就是求A点上方的函数图象对应的x的取值范围,据图写出即可;
(3)分点![]() 在点
在点![]() 的左侧和右侧考虑,构造图形,利用三角形的中位线即可求出点
的左侧和右侧考虑,构造图形,利用三角形的中位线即可求出点![]() 的坐标.
的坐标.
解:(1)设反比例函数表达式为![]() ,
,
∵此函数过![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴此函数表达式是![]() .
.
(2)∵点![]() 在反比例函数
在反比例函数![]() 的第一象限的图象上,∴
的第一象限的图象上,∴![]() ,且
,且![]() ,
,
∵![]() ,∴
,∴![]() .
.
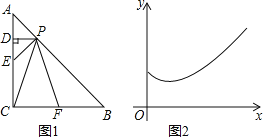
(3)当点![]() 在点
在点![]() 左边时,分别过点
左边时,分别过点![]() 、
、![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,如图1所示.
,如图1所示.
∵![]() ,
,![]() ,∴
,∴![]() 为
为![]() 的中位线,
的中位线,
∴![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴点![]() ;
;
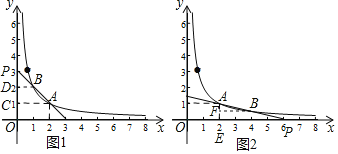
当点![]() 在点
在点![]() 的右边时,过点
的右边时,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中位线,如图2所示.
的中位线,如图2所示.
∴![]() ,∴点
,∴点![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴点![]() .
.
综上所述:点![]() 的坐标为(0,3)或(6,0).
的坐标为(0,3)或(6,0).

 名校课堂系列答案
名校课堂系列答案【题目】已知![]() 是
是![]() 的函数,如表是
的函数,如表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.
之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:

(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①![]() 对应的函数值
对应的函数值![]() 约为 ;
约为 ;
②该函数的一条性质: .
【题目】2022年将在北京﹣﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 | 队员1 | 队员1 | 队员1 | 队员1 | 队员1 | |
甲组 | 176 | 177 | 175 | 176 | 177 | 175 |
乙组 | 178 | 175 | 170 | 174 | 183 | 176 |
设两队队员身高的平均数依次为![]() ,
,![]() ,方差依次为
,方差依次为![]() ,
,![]() ,下列关系中正确的是( )
,下列关系中正确的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,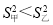 D.
D.![]() ,
,![]()