题目内容
如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
(1)梯形ABCD的面积等于______;
(2)当PQ∥AB时,P点离开D点的时间等于______秒;
(3)当P,Q,C三点构成直角三角形时,P点离开D点多少时间?
解:(1)36;
(2)分别延长BA和CD,交于点N,
则NA:NB=AD:BC,即
 =
=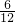
NA=5,则ND=NA=5.
设用了x秒PQ∥AB,则DP=x,PC=5-x,CQ=2x.
PC:CN=CQ:CB,
 ,x=
,x= .
.
即当PQ∥AB时,P点离开D点的时间等于 秒;
秒;
(3)当P,Q,C三点构成直角三角形时,有两种情况:

①当PQ⊥BC时,设P点离开D点x秒,
作DE⊥BC于E,∴PQ∥DE.
∴ ,
,
∴
∴当PQ⊥BC时,P点离开D点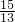 秒.
秒.
②当QP⊥CD时,设P点离开D点x秒
∵∠QPC=∠DEC=90°,∠C=∠C.
∴△QPC∽△DEC
∴

∴
∴当QP⊥CD时,点P离开点D 秒.
秒.
由①②知,当P,Q,C三点构成直角三角形时,点P离开点D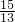 秒或
秒或 秒.
秒.
分析:(1)已知梯形各边的长,用勾股定理易求高以及其面积;
(2)本题要找出线段之比,设要用x秒后PQ∥AB,已知 ,求出x的值即可;
,求出x的值即可;
(3)本题有两种情况.当PQ⊥BC,利用 求解.第二种是当QP⊥CD时,设P点离开D点x秒,利用线段比求解.
求解.第二种是当QP⊥CD时,设P点离开D点x秒,利用线段比求解.
点评:本题涉及大量的线段比以及要靠辅助线的帮助才能求解,有一定难度,需认真分析.
(2)分别延长BA和CD,交于点N,

则NA:NB=AD:BC,即
 =
=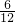
NA=5,则ND=NA=5.
设用了x秒PQ∥AB,则DP=x,PC=5-x,CQ=2x.
PC:CN=CQ:CB,
 ,x=
,x= .
.即当PQ∥AB时,P点离开D点的时间等于
 秒;
秒;(3)当P,Q,C三点构成直角三角形时,有两种情况:

①当PQ⊥BC时,设P点离开D点x秒,
作DE⊥BC于E,∴PQ∥DE.
∴
 ,
,
∴

∴当PQ⊥BC时,P点离开D点
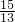 秒.
秒.②当QP⊥CD时,设P点离开D点x秒
∵∠QPC=∠DEC=90°,∠C=∠C.
∴△QPC∽△DEC
∴


∴

∴当QP⊥CD时,点P离开点D
 秒.
秒.由①②知,当P,Q,C三点构成直角三角形时,点P离开点D
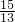 秒或
秒或 秒.
秒.分析:(1)已知梯形各边的长,用勾股定理易求高以及其面积;
(2)本题要找出线段之比,设要用x秒后PQ∥AB,已知
 ,求出x的值即可;
,求出x的值即可;(3)本题有两种情况.当PQ⊥BC,利用
 求解.第二种是当QP⊥CD时,设P点离开D点x秒,利用线段比求解.
求解.第二种是当QP⊥CD时,设P点离开D点x秒,利用线段比求解.点评:本题涉及大量的线段比以及要靠辅助线的帮助才能求解,有一定难度,需认真分析.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 在,求出这样的t的值;若不存在,请说明理由.
在,求出这样的t的值;若不存在,请说明理由. 10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE.
10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE. 已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD.
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD. (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
