Question

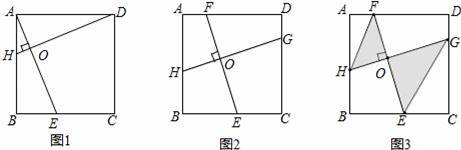
．如图，将矩形纸片ABCD沿EF折叠，使点B与CD的中点重合，若AB=2，BC=3，则△FCB′与△B′DG的面积之比为（　　）

A．9：4 B．3：2  C．4：3 D．16：9

Answer 1

D【考点】翻折变换（折叠问题）．

【专题】数形结合．

【分析】设BF=x，则CF=3﹣x，B'F=x，在Rt△B′CF中，利用勾股定理求出x的值，继而判断△DB′G∽△CFB′，根据面积比等于相似比的平方即可得出答案．

【解答】解：设BF=x，则CF=3﹣x，B'F=x，

又点B′为CD的中点，

∴B′C=1，

在Rt△B′CF中，B'F²=B′C²+CF²，即x²=1+（3﹣x）²，

解得：x=，即可得CF=3﹣=，

∵∠DB′G+∠DGB'=90°，∠DB′G+∠CB′F=90°，

∴∠DGB′=∠CB′F，

∴Rt△DB′G∽Rt△CFB′，

根据面积比等于相似比的平方可得： ===．

故选D．

【点评】此题考查了翻折变换的知识，解答本题的关键是求出FC的长度，然后利用面积比等于相似比的平方进行求解，难度一般．