题目内容
△ABC中,∠A,∠B均为锐角,且有|tan2B﹣3|+(2sinA﹣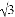 )2=0,则△ABC是( )
)2=0,则△ABC是( )
A. 直角(不等腰)三角形 B. 等边三角形
C. 等腰(不等边)三角形 D. 等腰直角三角形
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
△ABC中,∠A,∠B均为锐角,且有|tan2B﹣3|+(2sinA﹣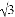 )2=0,则△ABC是( )
)2=0,则△ABC是( )
A. 直角(不等腰)三角形 B. 等边三角形
C. 等腰(不等边)三角形 D. 等腰直角三角形
 名校课堂系列答案
名校课堂系列答案