题目内容
4.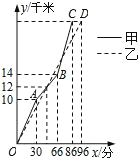 在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论:(1)甲先到达终点;(2)前30分钟,甲在乙的前面;(3)第48分钟时,两人第一次相遇;(4)这次比赛的全程是28千米,其中正确的个数是( )
在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论:(1)甲先到达终点;(2)前30分钟,甲在乙的前面;(3)第48分钟时,两人第一次相遇;(4)这次比赛的全程是28千米,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)根据图象可知甲骑完全程所用时间短,即(1)成立;
(2)结合OA段图象,甲的图象在乙的图象的上方,可知甲在乙的前面,(2)成立;
(3)利用待定系数法求出甲图象AB段的函数解析式,代入y=12,即可求出两人第一次相遇的时间,得出(3)成立;
(4)由第一次相遇的交点坐标可求出乙的速度,结合路程=速度×时间,可算出这次比赛的全程,由此判断出(4)不成立.结合(1)(2)(3)(4)即可得出结论.
解答 解:(1)C点横坐标为86,D点横坐标为96,
由86<96可知,甲先到达终点,(1)成立;
(2)图象OA段,甲的图象在乙的上方,
即前30分钟,甲在乙的前面,(2)成立;
(3)设AB段甲选手行驶的路程y关于时间x的函数关系式为y=kx+b,
将A、B点坐标代入,得$\left\{\begin{array}{l}{10=30k+b}\\{14=66k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{9}}\\{b=\frac{60}{9}}\end{array}\right.$,即函数关系式为y=$\frac{1}{9}$x+$\frac{60}{9}$.
令y=12,可得$\frac{1}{9}$x+$\frac{60}{9}$=12,解得:x=48,(3)成立;
(4)乙选手的速度为12÷48=$\frac{1}{4}$(千米/分),
次比赛的全程为$\frac{1}{4}$×96=24(千米),(4)不成立.
综上可知:(1)、(2)、(3)成立.
故选C.
点评 本题考查了一次函数的应用,解题的关键是根据图象结合数量关系逐条分析4条结论.本题属于基础题,难度不大,解决给题型题目,数形结合是关键.

| A. | a3+a3=a6 | B. | 4ab÷2a=2ab | C. | a3•a4=a7 | D. | (3x2)3=9x6 |
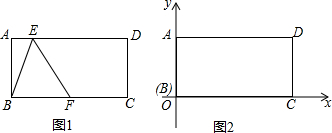
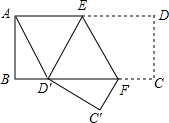 如图,四边形ABCD是矩形,AB=2,将矩形ABCD沿EF折叠,点D落在BC边的D′处.若四边形AD′FE恰好为菱形,则矩形的边AD的长度为$\frac{8\sqrt{3}}{3}$.
如图,四边形ABCD是矩形,AB=2,将矩形ABCD沿EF折叠,点D落在BC边的D′处.若四边形AD′FE恰好为菱形,则矩形的边AD的长度为$\frac{8\sqrt{3}}{3}$.