题目内容
(1)计算
(2)解方程 .
.
解:(1)原式= ×
× -
-
= -
-
= ,
,
(3)原式可化为: ,
,
方程两边同乘以(x-3)(x-1),
得:x(x-1)-2(x-3)=(x-3)(x-1),
解得:x=-3,
经检验,x=-3是原方程的根,
∴x=-3.
分析:(1)先对分式进行化简,然后根据分式的运算法则计算即可得出结果,
(2)先对分式进行化简,然后方程两边同乘以(x-3)(x-1),计算即可得出结果.
点评:本题主要考查了分式的运算法则及解分式方程的一般方法,需要认真进行注意检验,难度适中.
 ×
× -
-
=
 -
-
=
 ,
,(3)原式可化为:
 ,
,方程两边同乘以(x-3)(x-1),
得:x(x-1)-2(x-3)=(x-3)(x-1),
解得:x=-3,
经检验,x=-3是原方程的根,
∴x=-3.
分析:(1)先对分式进行化简,然后根据分式的运算法则计算即可得出结果,
(2)先对分式进行化简,然后方程两边同乘以(x-3)(x-1),计算即可得出结果.
点评:本题主要考查了分式的运算法则及解分式方程的一般方法,需要认真进行注意检验,难度适中.

练习册系列答案
相关题目
甲、乙两人参加射击选拔赛,各射击了5次,成绩如下表(单位:环):
甲、乙两人射击成绩统计表
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲 | 9 | 4 | 7 | 4 | 6 |
| 乙 | 7 | 5 | 7 | 4 | 7 |
小明计算了甲射击成绩的平均数和方差:
解: = = (9+4+7+4+6)=6(环); (9+4+7+4+6)=6(环);s2甲=  [(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2] [(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]=  (9+4+1+4+0) (9+4+1+4+0)=3.6(环2) |
(1)请参照小明的计算方法,求乙射击成绩的平均数与方差;
(2)请你从平均数和方差的角度进行分析,谁将被选中.
 某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了尚不完善的统计表,并计算了甲成绩的平均数和方差(见小宇的作业).
某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了尚不完善的统计表,并计算了甲成绩的平均数和方差(见小宇的作业).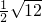 -(5-π)0+2tan60°
-(5-π)0+2tan60° =
=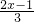 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据. =
= .
. -(5-π)+2tan60°
-(5-π)+2tan60° =
= 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据. =
= ______去分母,得3(3x+5)=2(2x-1).去括号,得9x+15=4x-2.______,得9x-4x=-15-2.______合并,得5x=-17.______,得x=-
______去分母,得3(3x+5)=2(2x-1).去括号,得9x+15=4x-2.______,得9x-4x=-15-2.______合并,得5x=-17.______,得x=- .
.