题目内容
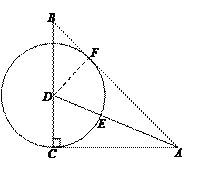
【题目】如图,在Rt△ABC中,∠C![]() 90°,AC
90°,AC![]() BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
(1)判断直线AB与⊙D的位置关系并证明.
(2)若AC![]() 1,求
1,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]()
【解析】分析:(1)根据“作垂直,证相等”可证明AB与⊙D相切;
(2)分别求出![]() 所在圆的半径和圆心有的度数,代入弧长公式进行计算即可得解.
所在圆的半径和圆心有的度数,代入弧长公式进行计算即可得解.
详解:(1)AB与⊙D相切.
证明:过点D作DF⊥AB,垂足为F.
∵AD是Rt△ABC的角平分线,∠C![]() 90°,
90°,
∴DF![]() DC,
DC,
即d![]() r,
r,
∴AB与⊙D相切.
(2)∵∠C![]() 90°,AC
90°,AC![]() BC
BC![]() 1,∴∠BAC
1,∴∠BAC![]() ∠B
∠B![]() 45°,AB
45°,AB![]() .
.
∵DF⊥AB,∴∠BDF![]() ∠B
∠B![]() 45°,∴BF
45°,∴BF![]() DF.
DF.
∵AB、AC分别与⊙D相切,∴AF![]() AC
AC![]() 1.
1.
设⊙D的半径为r.易得BF![]() ,BD
,BD![]() ,
,
∴![]() ,∴r
,∴r![]() .
.
∵AD是Rt△ABC的角平分线,∠BAC![]() 45°,
45°,
∴∠DAC![]()
![]() ∠BAC
∠BAC![]() 22.5°.
22.5°.
又∵∠C![]() 90°,∴∠CDE
90°,∴∠CDE![]() 67.5°.
67.5°.
∴![]() .
.

练习册系列答案
相关题目