题目内容
【题目】已知,数轴上点![]() 、
、![]() 对应的数分别为
对应的数分别为![]() 、
、![]() ,且满足
,且满足![]() ,点
,点![]() 对应点的数为-3.
对应点的数为-3.
(1)![]() ______,
______,![]() ______;
______;
(2)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发向右运动,点
同时出发向右运动,点![]() 的速度为3个单位长度/秒;点
的速度为3个单位长度/秒;点![]() 的速度为1个单位长度/秒,求经过多长时间
的速度为1个单位长度/秒,求经过多长时间![]() 、
、![]() 两点的距离为
两点的距离为![]() ;
;
(3)在(2)的条件下,若点![]() 运动到点
运动到点![]() 立刻原速返回,到达点
立刻原速返回,到达点![]() 后停止运动,点
后停止运动,点![]() 运动至点
运动至点![]() 处又以原速返回,到达点
处又以原速返回,到达点![]() 后又折返向
后又折返向![]() 运动,当点
运动,当点![]() 停止运动点
停止运动点![]() 随之停止运动.求在整个运动过程中,两点
随之停止运动.求在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数.
同时到达的点在数轴上表示的数.

【答案】(1)-7,1.(2)经过![]() 秒或
秒或![]() 秒
秒![]() ,
,![]() 两点的距离为
两点的距离为![]() .(3)在整个运动过程中,两点
.(3)在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数分别是-1,0,-2.
同时到达的点在数轴上表示的数分别是-1,0,-2.
【解析】
(1)由绝对值和偶次方的非负性列方程组可解;
(2)设经过t秒两点的距离为![]() ,根据题意列绝对值方程求解即可;
,根据题意列绝对值方程求解即可;
(3)分类讨论:点P未运动到点C时;点P运动到点C返回时;当点P返回到点A时.分别求出不同阶段的运动时间,进而求出相关点所表示的数即可.
(1)由非负数的性质可得:![]() ,
,
∴![]() ,
,![]() ,
,
故答案为:-7,1;
(2)设经过![]() 秒两点的距离为
秒两点的距离为![]() ,
,
由题意得:![]() ,
,
解得![]() 或
或![]() ,
,
答:经过![]() 秒或
秒或![]() 秒
秒![]() ,
,![]() 两点的距离为
两点的距离为![]() ;
;
(3)点![]() 未运动到点
未运动到点![]() 时,设经过
时,设经过![]() 秒
秒![]() ,
,![]() 相遇,
相遇,
由题意得:![]() ,
,
∴![]() ,
,
表示的数为:![]() ,
,
点![]() 运动到点
运动到点![]() 返回时,设经过
返回时,设经过![]() 秒
秒![]() ,
,![]() 相過,
相過,
由题意得:![]() ,
,
∴![]() ,
,
表示的数是:![]() ,
,
当点![]() 返回到点
返回到点![]() 时,用时
时,用时![]() 秒,此时点
秒,此时点![]() 所在位置表示的数是
所在位置表示的数是![]() ,
,
设再经过![]() 秒相遇,
秒相遇,
由题意得:![]() ,
,
∴![]() ,
,
表示的数是:![]() ,
,
答:在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数分别是-1,0,-2.
同时到达的点在数轴上表示的数分别是-1,0,-2.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
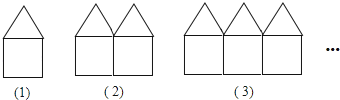
(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?