题目内容
6.已知一次函数y=kx+b的图象过点(-1,0)和点(0,2),若x(kx+b)<0,则x的取值范围是-1<x<0.分析 先确定直线y=kx+b和直线y=x与x轴的交点坐标,然后找出它们分别在x轴上方和在x轴下方所对应的自变量的范围即可.
解答 解:当-1<x<0时,函数y=kx+b在x轴上方,而直线y=x在x轴下方,
所以当-1<x<0时,x(kx+b)<0.
故答案为-1<x<0.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列调查方式中,适合用普查方式的是( )
| A. | 要了解一批等灯泡的使用寿命 | |
| B. | 要了解栾城电视台“栾城新闻”的收视率 | |
| C. | 要了解某校篮球队12名队员的身高状况 | |
| D. | 要了解全国人民对“春节连欢晚会”的满意度 |
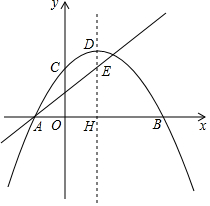 已知:如图,抛物线y=-$\frac{1}{4}$(x-h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=$\frac{3}{4}$x+$\frac{3}{2}$经过点A与对称轴交于E,点E的纵坐标为3.
已知:如图,抛物线y=-$\frac{1}{4}$(x-h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=$\frac{3}{4}$x+$\frac{3}{2}$经过点A与对称轴交于E,点E的纵坐标为3.



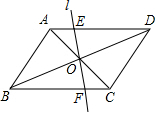 在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.
在?ABCD中,AB=6,BC=8,∠ABC=60°,AC、BC交于点O,过点O作任意l交AD于点E,交BC于点F(除端点外),则四边形ABFE周长的最小值为14+3$\sqrt{3}$.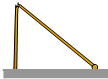 如图,一旗杆被大风刮断,旗杆的顶部着地点到旗杆底部的距离为4m,折断点离旗杆底部的高度为3m,则旗杆的高度为8m.
如图,一旗杆被大风刮断,旗杆的顶部着地点到旗杆底部的距离为4m,折断点离旗杆底部的高度为3m,则旗杆的高度为8m. 如图,△DAF≌△DBE,如果DF=7cm,AD=15cm,则AE=8cm.
如图,△DAF≌△DBE,如果DF=7cm,AD=15cm,则AE=8cm.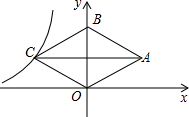 如图,在平面直角坐标系中,菱形OABC的顶点O是原点,顶点B在y轴正半轴上,顶点A在第一象限,菱形的两条对角线长分别是6和4,函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,菱形OABC的顶点O是原点,顶点B在y轴正半轴上,顶点A在第一象限,菱形的两条对角线长分别是6和4,函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )