题目内容
7. (1)如图,把∠AOB绕着O点按逆时针方向旋转一个角度,得∠A′OB′,指出图中所有相等的角.
(1)如图,把∠AOB绕着O点按逆时针方向旋转一个角度,得∠A′OB′,指出图中所有相等的角.(2)如图,BD平分∠ABC,BE分∠ABC成2:5两部分,∠DBE=21°,求∠ABC的度数.
分析 (1)由旋转的性质即可得到结论;
(2)先BE分∠ABC分2:5两部分的其中一份为x°然后再利用题中的关系求出∠DBE的值,从而可得关于α的方程,解出即可得出答案.
解答 解:(1)由旋转的性质得到∠AOB=∠A′OB′,∠AOA′=∠BOB′;
(2)设BE分∠ABC分2:5两部分的其中一份为x°,
由题意得2x+21=5x-21,
解得x=14,
所以∠ABC=14°×7=98°.
点评 本题考查了角平分线的定义,解题的关键是设未知数,然后找出题中的等量关系解未知数.

练习册系列答案
相关题目
17.有理数-3.14,0,|$-(-3\frac{1}{3})$|,-|-2009|,-(-1)中,最小的数是( )
| A. | -3.14 | B. | 0 | C. | |$-(-3\frac{1}{3})$| | D. | -|-2009| |
18.已知(x-3)2+$\sqrt{y+1}$=0,则x+y的值为( )
| A. | 2 | B. | -1 | C. | 1 | D. | 5 |
2.在锐角的内部引射线,当n=1,n=2时,图中小于180°角的个数及规律如表,请你在表中空白处填出射线为3和n的情形.
| 图形 |  | 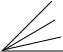 | 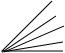 | 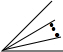 |
| n | 1 | 2 | 3 | n |
| 个数及规律 | 3=1+2=$\frac{2×3}{2}$ | 6=1+2+3=$\frac{3×4}{2}$ | 10=1+2+3+4=$\frac{4×5}{2}$ | 1+2+3+…+n+1=$\frac{(n+1)(n+2)}{2}$. |
12. 一副三角尺拼成如图所示的图案,则∠ABC的大小为( )
一副三角尺拼成如图所示的图案,则∠ABC的大小为( )
 一副三角尺拼成如图所示的图案,则∠ABC的大小为( )
一副三角尺拼成如图所示的图案,则∠ABC的大小为( )| A. | 100° | B. | 110° | C. | 120° | D. | 135° |
17. 如图,△ABC中,∠B,∠C的平分线相交于点O,过点O作DE∥BC,若AB=4,AC=3,则△ADE的周长是( )
如图,△ABC中,∠B,∠C的平分线相交于点O,过点O作DE∥BC,若AB=4,AC=3,则△ADE的周长是( )
 如图,△ABC中,∠B,∠C的平分线相交于点O,过点O作DE∥BC,若AB=4,AC=3,则△ADE的周长是( )
如图,△ABC中,∠B,∠C的平分线相交于点O,过点O作DE∥BC,若AB=4,AC=3,则△ADE的周长是( )| A. | 3 | B. | 4 | C. | 7 | D. | 不能确定 |
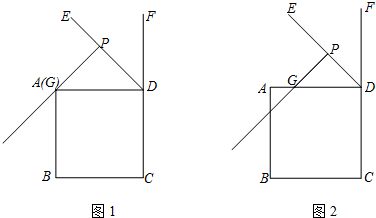
 如图,BD是△ABC的角平分线,DE⊥AB于点E.△ABC的面积为20,AB=12,BC=8,则DE的长为2.
如图,BD是△ABC的角平分线,DE⊥AB于点E.△ABC的面积为20,AB=12,BC=8,则DE的长为2.