题目内容
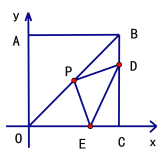
【题目】如图，在一个20米高的楼顶上有一信号塔DC，某同学为了测量信号塔的高度，在地面的A处测得信号塔下端D的仰角为30°，然后他正对塔的方向前进了8米到达地面的B处，又测得信号塔顶端C的仰角为45°，CD⊥AB于点E，E、B、A在一条直线上．信号塔CD的高度是多少？
【答案】20
-28
【解析】分析：利用30°的正切值即可求得AE长，进而可求得CE长．CE减去DE长即为信号塔CD的高度．
详解：根据题意得：AB=8米，DE=20米，∠A=30°，∠EBC=45°，
在Rt△ADE中，AE=DE=20米，
∴BE=AE﹣AB=20﹣8（米），
在Rt△BCE中，CE=BEtan45°=（20﹣8）×1=20﹣8（米），
∴CD=CE﹣DE=20﹣8﹣20=20﹣28（米）．
练习册系列答案
阅读快车系列答案
相关题目
