Question

【题目】综合与实践动手操作：用矩形下的折叠会出现等腰三角形，快速求BF的长．

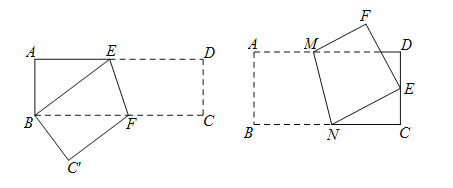
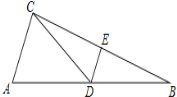
（1）如图，在矩形ABCD中，AB=3，AD=9，将此矩形折叠，使点D与点B重合，折痕为EF，则等腰三角形是 ；

（2）利用勾股定理建立方程，求出BF的长是多少？

（3）拓展：将此矩形折叠，使点B与DC的中点E重合，请你利用添加辅助线的方法，求AM的长；

Answer 1

【答案】（1）是等腰三角形；（2）；（3）AM的长为.

【解析】

（1）证明可知，即是等腰三角形；（2）可设，则，在中，根据勾股定理可求解；（3）连接ME，可设,则，在根据勾股定理分别表示出

，等量代换，可得x的值，即AM的长.

（1）是等腰三角形

四边形ABCD是矩形

由折叠的性质得：

是等腰三角形

（2）设，则

在中，根据勾股定理得

解得

（3）连接ME，设,则，由折叠性质得

E为DC的中点

在中，根据勾股定理得

在中，根据勾股定理得

解得

所以AM的长为