Question

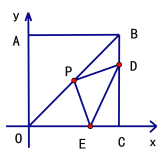
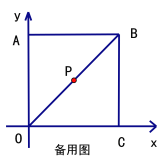
【题目】在直角坐标系中，正方形OABC的边长为8，连结OB，P为OB的中点.

（1）直接写出点B的坐标B（ ， ）

（2）点D从B点出发，以每秒1个单位长度的速度在线段BC上向终点C运动，连结PD，作PD⊥PE，交OC于点E，连结DE.设点D的运动时间为秒.

①点D在运动过程中，∠PED的大小是否发生变化？如果变化，请说明理由如果不变，求出∠PED的度数

②连结PC，当PC将△PDE分成的两部分面积之比为1:2时，求的值.

Answer 1

【答案】（1）8，8；（2）①∠PED的大小不变，∠PED=45°；②t的值为：秒或秒．

【解析】

（1）根据正方形的边长为8和正方形的性质写出点B的坐标；
（2）①如图1，作辅助线，证明四边形PMCN是正方形，再证明△DPN≌△EPM（ASA），可得△DPE是等腰直角三角形，可得结论；
②分两种情况：当PC将△PDE分成的两部分面积之比为1：2时，即G是ED的三等分点，根据面积法可知：EC与CD的比为1：2或2：1，列方程可得结论．

解：（1）∵正方形OABC的边长为8，
∴B（8，8）；
故答案为：8，8；

（2）①∠PED的大小不变；理由如下：
作PM⊥OC于M，PN⊥CB于N，如图1所示：

∵四边形OABC是正方形，
∴OC⊥BC，
∴∠MCN=∠PMC=∠PNC=90°，
∴四边形PMCN是矩形，
∵P是OB的中点，
∴N、M分别是BC和OC的中点，
∴MC=NC，
∴矩形PMCN是正方形，
∴PM=PN，∠MPN=90°，
∵∠DPE=90°，
∴∠DPN=∠EPM，
∵∠PND=∠PME=90°，
∴△DPN≌△EPM（ASA），
∴PD=PE，

∴△DPE是等腰直角三角形，
∴∠PED=45°；
②如图2，作PM⊥OC于M，PN⊥CB于N，

若PC将△PDE的面积分成1：2的两部分，
设PC交DE于点G，则点G为DE的三等分点；
当点D到达中点之前时，如图2所示，CD=8-t，
由△DPN≌△EPM得：ME=DN=4-t，

∴EC=CM-ME=4-（4-t）=t，
∵点G为EF的三等分点，
∴或
∵CP平分∠OCB，
∴或2，
即CD=2CE或CE=2CD，
∴8-t=2t或t=2（8-t），
t=或（舍）；

当点D越过中点N之后，如图3所示，CD=8-t，

由△DPN≌△EPM得：CD=8-t，DN=t-4
∴EC=CM+ME=4+（t-4）=t，
∵点G为EF的三等分点，
∴或
∵CP平分∠OCB，
∴或2，
即CD=2CE或CE=2CD，

∴8-t=2t或t=2（8-t），
t=（舍）或；
综上所述，当PC将△PED分成的两部分的面积之比为1：2时，t的值为：秒或秒．