Question

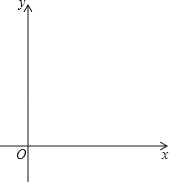
【题目】如图，△ABC的顶点坐标分别为A（﹣4，5），B（﹣5，2），C（﹣3，4）

（1）画出与△ABC关于原点O对称的△A1B1C1，并写出点A1的坐标为　 　；

（2）D是x轴上一点，使DB+DC的值最小，画出点D（保留画图痕迹）；

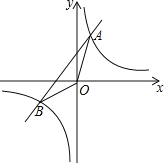
（3）P（t，0）是x轴上的动点，将点C绕点P顺时针旋转90°至点E，直线y＝﹣2x+5经过点E，则t的值为　 　．

Answer 1

【答案】（1）（4，﹣5）;（2）见解析；（3）﹣2．

【解析】

（1）利用关于原点对称点的坐标性质得出对应点位置进而得出答案.

（2）两点之间直线最短，作点B关于x轴的对称点B′，连接CB′交x轴得点.

（3）作CH⊥x轴于H，EK⊥x轴于K.证明△PCH≌△EPK，所以PK＝CH＝4，EK＝PH＝t+3，OK＝4+t，得点E在直线y＝﹣2x+5上，再代入直线y＝﹣2x+5即可求解.

解：（1）△A1B1C1如图所示，A1（4，﹣5）；

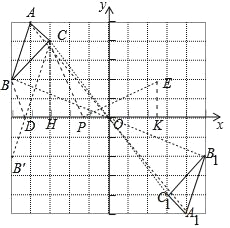
故答案为（4，﹣5）．

（2）作点B关于x轴的对称点B′，连接CB′交x轴于点D，此时BD+CD的值最小；

（3）作CH⊥x轴于H，EK⊥x轴于K．

∵∠CHP＝∠CPE＝∠PKE＝90°，

∴∠CPH+∠HCP＝90°，∠CPH+∠EPK＝90°，

∴∠PCH＝∠EPK，∵PC＝PE，

∴△PCH≌△EPK（AAS），

∴PK＝CH＝4，EK＝PH＝t+3，

∴OK＝4+t，

∴E（4+t，t+3），

∵点E在直线y＝﹣2x+5上，

∴t+3＝﹣2（4+t）+5，

t＝﹣2，

故答案为﹣2．