Question

【题目】感知：如图①，在等腰直角△ABC中，分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF，连结点D、E、F，则易知△DEF为等腰三角形．如果AB＝AC＝7，请直接写出△DEF的面积为　 　．

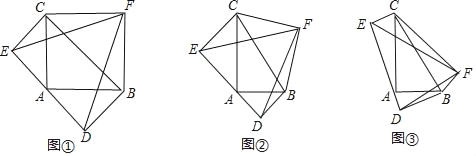
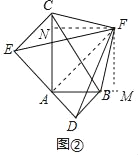
探究：如图②，Rt△ABC中，AB＝14，AC＝30，分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF，连结点D、E、F，求△DEF的面积为多少．

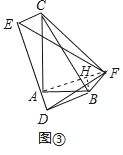
拓展：如图③，Rt△ABC中，AB＝14，AC＝15，分别以△ABC的三条边为斜边向△ABC外部作Rt△ABD、Rt△ACE、Rt△BCF，且tan∠BCF＝tan∠CAE＝tan∠ABD＝，连结点D、E、F，则△DEF的面积为　 　．

Answer 1

【答案】感知： 49;探究： 484;拓展： 168.15．

【解析】

感知：只要证明E、A、D共线，FA⊥DE，想办法求出DE、AF即可；

探究：如图②中，连接AF．作FM⊥AB于M，FN⊥AC于N．解法类似；

拓展：如图③中，连接AF，作BH⊥AF于H．解法类似；

解：感知：如图①中，连接AF．

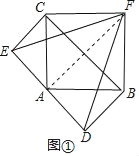
∵AC＝AB，∠BAC＝90°，△ACE，△ABD都是等腰直角三角形，

∴EC＝AE＝AD＝BD，∠CAE＝∠BAD＝45°

∴∠CAE+∠CAB+∠BAD＝180°，

∴E、A、D共线，

∵CF＝FB，∠FCE＝∠FBD，CE＝BD，

∴△CFE≌△BFD，

∴FE＝FD，∵AE＝AD，

∴FA⊥DE，

∴

探究：如图②中，连接AF．作FM⊥AB于M，FN⊥AC于N．

同理可证E、A、D共线，

∵∠BAC+∠CFB＝180°，

∴A、B、F、C四点共圆，

∴∠FAB＝∠FCB＝45°，∵∠BAD＝45°，

∴∠FAD＝90°，

∴FA⊥DE，

∵∠FAC＝∠FAB，FM⊥AB于M，FN⊥AC于N．

∴FN＝FM，

∵FC＝FB，

∴△FCN≌△FBM，

∴FN＝FM＝AM＝AN，CN＝BM，

∴AN+AM＝AC﹣CN+AM﹣BM＝44，

∴AM＝FM＝22，

∴

∴

（3）拓展：如图③中，连接AF，作BH⊥AF于H．

同法可证E、A、D共线，AF⊥DE，

易知：

由△FHB∽△CAB，可得：

∴

∴

∴

故答案为49，484，168.15．