题目内容
【题目】如图，正方形 ABCD 中，AE=AB，直线 DE 交 BC 于点 F，则∠BED 的度数是（ ）
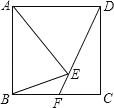
A. 105° B. 120° C. 135° D. 150°
【答案】C
【解析】
先设∠BAE=x°，根据正方形性质推出 AB=AE=AD，∠BAD=90°，根据等腰三角形性质和三角形的内角和定理求出∠AEB 和∠AED 的度数．
解：设∠BAE=x°，
∵四边形 ABCD 是正方形，
∴∠BAD=90°，AB=AD，
∵AE=AB，
∴AB=AE=AD，
∴∠ABE=∠AEB=
（180°﹣∠BAE）=90°﹣x°，
∴∠DAE=90°﹣x°
∴∠AED=∠ADE= （180°﹣∠DAE）= [180°﹣（90°﹣x°）]=45°+ x°，
∴∠BED=90°﹣x°+45°+ x°=135°．
故选：C．
练习册系列答案
优学名师名题系列答案
相关题目
