题目内容
10.已知关于x的函数y=mx2-x-(m-1).(1)m=0时,y=mx2-x-(m-1)是一次函数;
(2)求证:对任何实数m,y=mx2-x-(m-1)的图象与x都有公共点;
(3)若是关于x的二次函数y=mx2-x-(m-1)的图象与x有两个不同的公共点A、B(点A在点B左边),图象顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,y=mx2-x-(m-1)的图象都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
分析 (1)要使y=mx2-x-(m-1)是一次函数,需有m=0;
(2)当m=0时,y=-x+1,与x轴有交点,当m≠0时,求出△,进行判断;
(3)先求出二次函数与x轴的交点,然后求出AB的长度,根据△ABC为等腰直角三角形,可得AB=2|yc|,列出等式,求出m的值;
(4)先对二次函数进行因式分解,然后找出P点.
解答 解:(1)当m=0时,
y=mx2-x-(m-1)=-x+1为一次函数;
(2)当m=0时,y=-x+1与x轴交于点(1,0),
当m≠0时,△=(-1)2+4m(m-1)=(2m-1)2≥0,
故对任何实数m,y=mx2-x-(m-1)的图象与x都有公共点;
(3)∵二次函数与x有两个不同的公共点A、B,
∴△=(2m-1)2>0,
∴m≠$\frac{1}{2}$,
令mx2-x-(m-1)=0,
解得:x1=1,x2=-$\frac{m-1}{m}$,
∴AB=|1+$\frac{m-1}{m}$|=|$\frac{2m-1}{m}$|,
顶点C的纵坐标为:yc=$\frac{-4m(m-1)-1}{4m}$,
∵△ABC为等腰直角三角形,
∴AB=2|yc|,
即|$\frac{2m-1}{m}$|=2|$\frac{-4m(m-1)-1}{4m}$|,
解得:m1=-$\frac{1}{2}$,m2=$\frac{3}{2}$,m3=$\frac{1}{2}$(不合题意,舍去),
∴m的值为-$\frac{1}{2}$或$\frac{3}{2}$;
(4)y=mx2-x-(m-1)=[mx+(m-1)](x-1),
对任何实数m,当x=1时,y=0,
当mx+m=0时,x=-1,
此时y=2,
故点P的坐标为(1,0)或(-1,2).
故答案为:0.
点评 本题考查了二次函数的综合应用,涉及了抛物线与x轴的交点,等腰直角三角形以及二次函数的性质,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

| A. | -3 | B. | -5 | C. | 1或-3 | D. | 1或-5 |
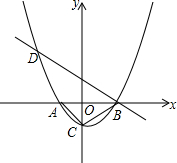 如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.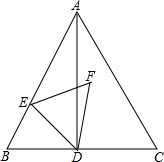 已知等边△ABC的边长为4,点D是边BC的中点,点E在线段BA上由点B向点A运动,连接ED,以ED为边在ED右侧作等边三角形EDF,设△EDF的中心为O,则点E由点B向点A运动的过程中,点O运动的路径长为$\frac{4\sqrt{3}}{3}$.
已知等边△ABC的边长为4,点D是边BC的中点,点E在线段BA上由点B向点A运动,连接ED,以ED为边在ED右侧作等边三角形EDF,设△EDF的中心为O,则点E由点B向点A运动的过程中,点O运动的路径长为$\frac{4\sqrt{3}}{3}$. 如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数.
如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数. 到直线l1、l2的距离相等的点的轨迹是什么?
到直线l1、l2的距离相等的点的轨迹是什么?